Advertisements
Advertisements
Question
Two circles touch each other externally. The sum of their areas is 74π cm2 and the distance between their centers is 12 cm. Find the diameters of the circle.
Solution
Let the radius of the circles be r1 and r2.
So, r1 + r2 = 12 ⇒ r2 = 12 - r1
Sum of the areas of the circles = 74π
⇒ πr12 + πr12 = 74π
⇒ r12 + r12 = 74
⇒ r12 + ( 12 - r1 )2 = 74
⇒ r12 + 144 - 24r1 + r12 = 74
⇒ 2r12 - 24r1 + 70 = 0
⇒ r12 - 12r1 + 35 = 0
⇒ ( r1 - 7 )( r1 - 5 ) = 0
⇒ r1 = 7 or r1 = 5
Ir r1 = 7 cm, then r2 = 5 cm
If r1 = 5 cm, then r2 = 7 cm
So, the diameters of the circles will 10 cm and 14 cm.
APPEARS IN
RELATED QUESTIONS
Find the area enclosed between two concentric circles of radii 3.5 cm and 7 cm. A third concentric circle is drawn outside the 7 cm circle , such that the area enclosed between it and the 7 cm circle is same as that between the two inner circles . Find the radius of the third circle correct to one decimal place.
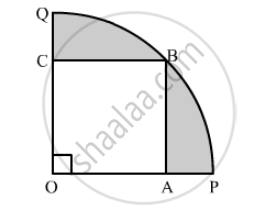
In the following figure a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 21 cm, find the area of the shaded region.
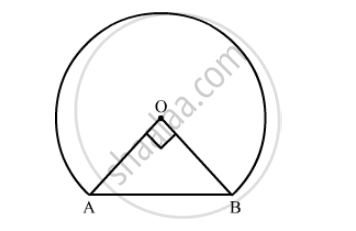
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the area of the cross-section.
If a chord of a circle of radius 28 cm makes an angle of 90 ° at the centre, then the area of the major segment is
Find the area of a ring whose outer and inner radii are respectively 23 cm and 12 cm.
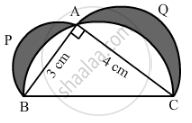
In the given figure, ∆ABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
The area of circle is equal to the sum of the areas of two circles of radii 24 cm and 7 cm. The diameter of the new circle is
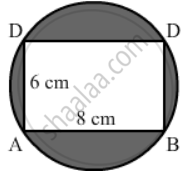
In the given figure, ABCD is a rectangle inscribed in a circle having length 8 cm and breadth 6 cm. If π = 3.14, then the area of the shaded region is:
The radii of two circles are in the ratio 3: 8. If the difference between their areas is 2695π cm2, find the area of the smaller circle.
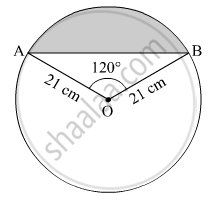
Find the area of the segment shown in Fig. 2, if the radius of the circle is 21 cm and ∠AOB = 120° `( "Use" π = (22)/(7))`