Advertisements
Advertisements
Question
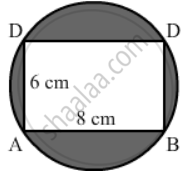
In the given figure, ABCD is a rectangle inscribed in a circle having length 8 cm and breadth 6 cm. If π = 3.14, then the area of the shaded region is:
Options
264 cm2
266 cm2
272 cm2
254 cm2
None of the above.
Solution
None of the above
Explanation:
All options are incorrect; the correct answer is 30.5 cm.
Join AC.
Now, AC is the diameter of the circle.
We have:
AC2 = AB2 + BC2 [By pythagoras' theorem]
⇒ AC2 = {(8)2 + (6)2} cm2
⇒ AC2 = (64 + 36) cm2
⇒ AC2 = 100 cm2
∴ Radius of the circle`=10/2 "cm"`
= 5 cm
Now,
Area of the shaded region = Area of the circle with radius 5 cm − Area of the rectangle ABCD
`=|(3.14xx5xx5)-(8xx6)| "cm"^2`
`=|(314/100xx25)-48| "cm"^2`
`=(157/2-48) "cm" ^2`
`=61/2 "cm" ^2`
= 30.5 cm2
APPEARS IN
RELATED QUESTIONS
A 80 m by 64 m rectangular lawn has two roads, each 5 m wide, running through its middle, one parallel to its length and the other parallel to its breadth. Find the cost of gravelling the reads at ₹` 40 per m^2`
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB=90° and AC = 15 cm.

In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the length of the boundary of the shaded region.
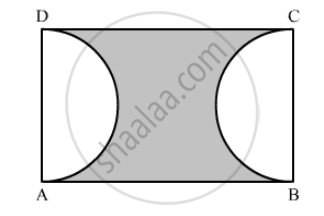
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
If a wire is bent into the shape of a square, then the area of the square is 81 cm2. When wire is bent into a semi-circular shape, then the area of the semi-circle will be ______.
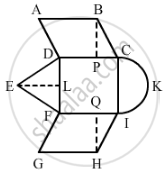
A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure.
The area of circle is equal to the sum of the areas of two circles of radii 24 cm and 7 cm. The diameter of the new circle is
The minute hand of a clock is 12 cm long. Find the area of the face of the clock described by the minute hand in 35 minutes.
The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below.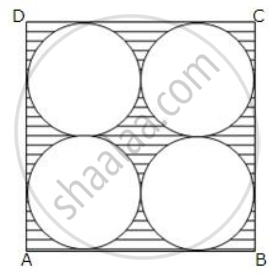
Find the area of the remaining card-board.
A circular park is surrounded by a road 21 m wide. If the radius of the park is 105 m, find the area of the road.
