Advertisements
Advertisements
Question
A metal wire, when bent in the form of an equilateral triangle of largest area, encloses an area of 484 `sqrt3` cm2. If the same wire is bent into the form of a circle of largest area, find the area of this circle.
Solution
Let 'a' be the length of each side of an equilateral triangle formed.
Now, the area of an equilateral triangle formed = 484√3 cm2
⇒ `sqrt3/4`a2 = 484√3
⇒ a2 = 4 x 484
⇒ a = 2 x 22 = 44 cm
Then, perimeter of equilateral triangle = 3a = 3 x 44 = 132 cm
Now, length of wire = perimeter of equilateral triangle = circumference of circle
⇒ circumference of circle = 132 cm
⇒ 2πr = 132 .....( r is radius of circle )
⇒ r = `[ 132 xx 7 ]/[ 2 xx 22 ]` = 21 cm
∴ Area of circle = πr2 = `22/7` x 21 x 21 = 1386cm2.
APPEARS IN
RELATED QUESTIONS
In Figure, find the area of the shaded region [Use π = 3.14]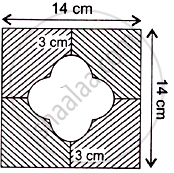
Four equal circles, each of radius a units, touch each other. Show that the area between them is `(6/7"a"^2)` sq units.
A bucket is raised from a well by means of a rope wound round a wheel of diameter 35 cm. If the bucket ascends in 2 minutes with a uniform speed of 1.1 m per sec, calculate the number of complete revolutions the wheel makes in raising the bucket.
The cost of fencing a circular field at the rate of ₹ 240 per meter is ₹ 52,800. The field is to be ploughed at the rate of ₹ 12.50 per m2. Find the cost of pouching the field.
The diameter of a circle is 5.6 cm. Find its circumference.
The circumference of a circle is equal to the perimeter of a square. The area of the square is 484 sq.m. Find the area of the circle.
A wire in the form of a circle of radius 42cm. It is bent into a square. Determine the side of the square and compare the area of the regions enclosed in the two cases.
Formula used to find the circumference of a circle is
A circular pond is surrounded by a 2 m wide circular path. If outer circumference of circular path is 44 m, find the inner circumference of the circular path. Also find area of the path.
The circumferences of two circles are in the ratio 4 : 5. What is the ratio of their radii?
