Advertisements
Advertisements
Question
A circular pond is surrounded by a 2 m wide circular path. If outer circumference of circular path is 44 m, find the inner circumference of the circular path. Also find area of the path.
Advertisements
Solution
Let R and r be the radius of outer circle and inner circle, respectively.
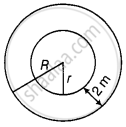
It is given that, circumference of outer circle is 44 m.
∴ 2πR = 44 ...[∵ Circumference of circle = 2πr]
⇒ `2 xx 22/7 xx R = 44`
⇒ `R = 44/(2 xx 22/7) = (7 xx 44)/(2 xx 22) = 7 m`
Since, r = (R – 2) m = (7 – 2) m = 5 m
∴ Inner circumference of the circular path = 2πr
= `2 xx 22/7 xx 5`
= 31.43 m (approx.)
∵ Area of path = Area of outer circle – Area of inner circle
= π(R2 – r2)
= `22/7 (7^2 - 5^2)`
= `22/7 xx 24`
= 75.43 m2 (approx.)
APPEARS IN
RELATED QUESTIONS
A wire is looped in the form of a circle of radius 28 cm. It is re-bent into a square form. Determine the length of the side of the square.
An arc of a circle is of length 5π cm and the sector it bounds has an area of 20 π cm2. Find the radius of the circle.
The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet. (Take π = 3.14)
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that Perimeter of shaded region is 𝑟 (tan 𝜃 + sec 𝜃 +`(pitheta)/180`− 1)
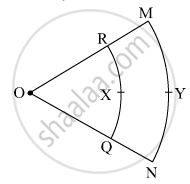
In the given figure, O is the centre of the sector. \[\angle\]ROQ = \[\angle\]MON = 60° . OR = 7 cm, and OM = 21 cm. Find the lengths of arc RXQ and arc MYN. (\[\pi = \frac{22}{7}\])
A conical tent with a capacity of 600 m3 stands on a circular base of area 160 m2 Find in m2 the area of the canvas.
A wire is in the form of a circle of radius 42 cm. It is bent into a square.
Determine the side of the square and compare the area of the regions enclosed in two cases.
Find the dimensions of a rectangular park whose perimeter is 60 m and area 200 m2.
The circumference of a circle exceeds its diameter by 18 cm. find the radius of the circle.
