Advertisements
Advertisements
Question
The hypotenuse of a right-angled triangle is 65 cm and its base is 60 cm. Find the length of perpendicular and the area of the triangle.
Solution
Hypotenuse = 65 cm
Base = 60 cm
In a right angled triangle,
`"(Hypotenuse)"^2="(Base)"^2+"(Perpendicular)"^2`
⇒`(65)^2=(60)^2+"(perpendicular)"^2`
⇒ `(65)^2-(60)^2+"(perpendicular)"^2`
⇒`"(Perpendicular)"^2=(65-60)(65+60)`
⇒`"(Perpendicular)"=5xx125`
⇒`"(Perpendicular)"^2=625`
⇒`"(Perpendicular)"^2=25 cm`
`"Area of triangle"=1/2xx"Base"xx"perpendicular"`
=`1/2xx60xx25`
=`750cm^2`
APPEARS IN
RELATED QUESTIONS
A wire is looped in the form of a circle of radius 28 cm. It is re-bent into a square form. Determine the length of the side of the square.
Find the circumference of the circle with the following radius: (Take `bb(pi = 22/7`)
28 mm
The circumference of a circle exceeds diameter by 16.8 cm. Find the circumference of
circle.
The area of a minor sector of a circle is 3.85 cm2 and the measure of its central angle is 36°. Find the radius of the circle.
Diagonal of a square is 20 cm. Find the length and perimeter of the square.
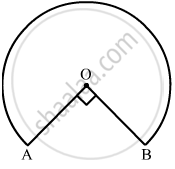
In the given figure, the shape of the top of a table is that of a sector of a circle with centre O and ∠AOB = 90°. If AO = OB = 42 cm,· then find the perimeter of the top of the table.
A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the area of the minor and major segments.
Find the area and perimeter of the following semi-circle :
Radius= 1.4 cm
Find the radius of the circle whose circumference is equal to the sum of the circumferences of the circles having radius 15 cm and 8 cm.
Circumferences of two circles are equal. Is it necessary that their areas be equal? Why?
