Advertisements
Advertisements
Question
In Figure, find the area of the shaded region [Use π = 3.14]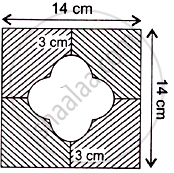
Solution
From the symmetry of the given figure, we have
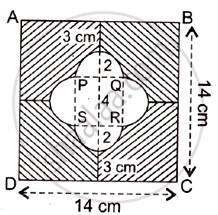
Let the radius of semicircle, r = `d/2 = 4/2 = 2cm` (Diameter of semicircle, d = `14/2 - 3` = 4 cm )
Let the side of small square = a = 4 cm (Side = Diameter of semicircle
Area of square ABCD = (Side)2 = (A)2 = (14)2 = 196cm2
Area of small square PQRS = (Side)2 = (a)2 = (4)2 = 16cm2
Area of 4 Semicircle = 4 x `1/2 pir^2`
= 4 x `1/2 xx 3.14 xx 2^2 = 25.12 cm^2`
∴ Required area = ( Area of big square – Area of small square – Area of 4 semicircles ) = ( 196 - 16 - 25.12 ) = 154.88 cm2
APPEARS IN
RELATED QUESTIONS
The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
Choose the correct alternative answer for the following question.
The curved surface area of a cylinder is 440 cm 2 and its radius is 5 cm. Find its height.
The circumference of a circle is 22 cm. Find the area of its quadrant.
The areas of two circles are in the ratio 4: 9. What is the ratio between their circumferences?
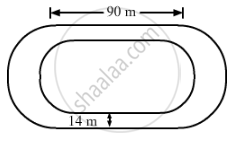
The inside perimeter of a running track shown in the figure is 400 m. The length of each of the straight portions is 90 m, and the ends are semicircles. If the track is 14 m wide everywhere, find the area of the track. Also, find the length of the outer boundary of the track.
Find the area and perimeter of the circle with the following :
Radius= 10.5 cm
Draw the circumcircle of Δ PMT in which PM = 5.4, P = 60°, M = 70°.
Each side of a square is 44 cm. Find its perimeter. If this perimeter is equal to the circumference of a circle, find the radius of the circle.
A circular racing track has inner circumference 528 m and outer circumference 616 m. Find the width of the track.
The circumference of a circle whose area is 81 πr2, is ______.
