Advertisements
Advertisements
प्रश्न
In Figure, find the area of the shaded region [Use π = 3.14]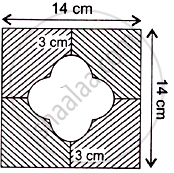
उत्तर
From the symmetry of the given figure, we have
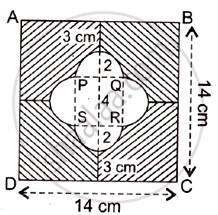
Let the radius of semicircle, r = `d/2 = 4/2 = 2cm` (Diameter of semicircle, d = `14/2 - 3` = 4 cm )
Let the side of small square = a = 4 cm (Side = Diameter of semicircle
Area of square ABCD = (Side)2 = (A)2 = (14)2 = 196cm2
Area of small square PQRS = (Side)2 = (a)2 = (4)2 = 16cm2
Area of 4 Semicircle = 4 x `1/2 pir^2`
= 4 x `1/2 xx 3.14 xx 2^2 = 25.12 cm^2`
∴ Required area = ( Area of big square – Area of small square – Area of 4 semicircles ) = ( 196 - 16 - 25.12 ) = 154.88 cm2
APPEARS IN
संबंधित प्रश्न
The side of a square is 10 cm. find the area of circumscribed and inscribed circles.
A car travels 1 km distance in which each wheel makes 450 complete revolutions. Find the radius of wheel.
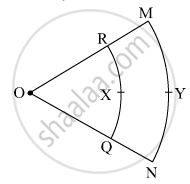
In the given figure, O is the centre of the sector. \[\angle\]ROQ = \[\angle\]MON = 60° . OR = 7 cm, and OM = 21 cm. Find the lengths of arc RXQ and arc MYN. (\[\pi = \frac{22}{7}\])
A wire is in the form of a circle of radius 42 cm. It is bent into a square.
Determine the side of the square and compare the area of the regions enclosed in two cases.
The circumference of a given circular park is 55 m. It is surrounded by a path of uniform width of 3.5 m. Find the area of the path.
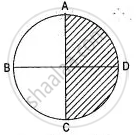
AC and BD are two perpendicular diameter of a circle ABCD. Given that the area of shaded portion is 308 cm2 calculate:
(i) The length of AC and
(ii) The circumference of circle
Find the circumference of the circle whose area is 25times the area of the circle with radius 7cm.
Diameters of different circles are given below. Find their circumference (Take π = `22/7`)
d = 70 cm
Find the total cost of wooden fencing around a circular garden of diameter 28 m, if 1 m of fencing costs ₹ 300.
The circumferences of two circles are in the ratio 4 : 5. What is the ratio of their radii?
