Advertisements
Advertisements
Question
Four equal circles, each of radius a units, touch each other. Show that the area between them is `(6/7"a"^2)` sq units.
Solution
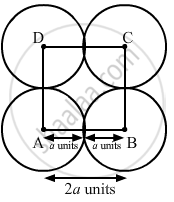
When four circles touch each other, their centres form the vertices of a square. The sides of the square are 2a units.
Area of the square = (2a)2 = 4a2 sq. units
Area occupied by the four sectors
`= 4xx90/360xxpixx"a"^2`
= πa2 sq. units
Area between the circles = Area of the square - Area of the four sectors
`=4xx90xx360xx"a"^2`
= πa2 sq. units
Area between the circles = Area of the square -- Area of the four sectors
`= (4 - 22/7)"a"^2`
`=6/7"a"^2 "sq". "units"`
APPEARS IN
RELATED QUESTIONS
The sum of the radii of two circles is 7 cm, and the difference of their circumferences is 8 cm. Find the circumference of the circles.
A race track is in the form of a rig whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.
The wheels of a car make 2500 revolutions in covering a distance of 4.95 km. Find the diameter of a wheel.
Find the diameter of the sphere for the following :
Surface Area = 221. 76 cm2
There are two circular gardens A and B. The circumference of garden A is 1.760 km and the area of garden B is 25 times the area of garden A. Find the circumference of garden B.
The circumference of a circle is 440 cm. Find its radius and diameter. (Take π = `22/7`)
The sum of the circumference and diameter of a circle is 176 cm. Find the area of the circle.
Find the circumference of the circles whose radii are given below.
91 mm
The diameter of the bullock cart wheel is 1.4 m. Find the distance covered by it in 150 rotations?
