Advertisements
Advertisements
प्रश्न
Four equal circles, each of radius a units, touch each other. Show that the area between them is `(6/7"a"^2)` sq units.
उत्तर
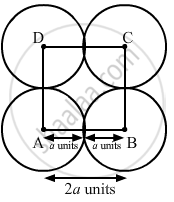
When four circles touch each other, their centres form the vertices of a square. The sides of the square are 2a units.
Area of the square = (2a)2 = 4a2 sq. units
Area occupied by the four sectors
`= 4xx90/360xxpixx"a"^2`
= πa2 sq. units
Area between the circles = Area of the square - Area of the four sectors
`=4xx90xx360xx"a"^2`
= πa2 sq. units
Area between the circles = Area of the square -- Area of the four sectors
`= (4 - 22/7)"a"^2`
`=6/7"a"^2 "sq". "units"`
APPEARS IN
संबंधित प्रश्न
Find the area of circle whose circumference is 44 cm.
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find Length of arc
The circumference of a circle is 22 cm. Find its area.
Sand from a cylindrical bucket 32 cm in height and 18 cm in radius is poured onto the ground making a conical heap 24 cm high. Find the radius of the conical heap.
The diameter of a wheel is 1.4m. How many revolutions does it make in moving a distance of 2.2 kms?
A wheel has a diameter of 84 cm. Find how many completer revolutions must it make to cover 3.168 km.
Find the area and perimeter of the circles with following: Diameter = 35cm
Find the circumference of a circle whose area is 81πcm2.
A bucket is raised from a well by means of a rope wound round a wheel of diameter 35 cm. If the bucket ascends in 2 minutes with a uniform speed of 1.1 m per sec, calculate the number of complete revolutions the wheel makes in raising the bucket.
The radius of the wheel of a bus is 0.7 m. How many rotations will a wheel complete while traveling a distance of 22 km?