Advertisements
Advertisements
Question
The area of rhombus is `480cm^2` , and one of its diagonal measures 48 cm. Find
(i) the length of the other diagonal,
(ii) the length of each of the sides
(iii) its perimeter
Solution
(i) Area of a rhombus, =` 1/2xxd_1xxd_2`, Where `d_1 and d_2` are the lengths of the diagonals.
⇒ `480=1/2xx48xxd_2`
⇒`d_2=(480xx2)/48`
⇒ `d_2=20 cm`
∴ Length of the other diagonal=`20cm`
(2) side=`1/2 sqrt(d_1^2-d_2^2)`
= `1/2sqrt(48^2+20^2)`
=`1/2sqrt(2304+400)`
=`1/2sqrt2704`
=`1/2xx52`
=`26 cm`
∴ Length of the side of the rhombus =`26cm`
(iii) Perimeter of the rhombus=`4xx"side"`
=`4xx26`
=`104 cm`
APPEARS IN
RELATED QUESTIONS
A field is in the form of circle. A fence is to be erected around the field. The cost of fencing would to Rs. 2640 at rate of Rs.12 per metre. Then the field is to be thoroughs ploughed at cost of Rs. 0.50 per m2. What is amount required to plough the field?
A race track is in the form of a rig whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.
The side of a square is 10 cm. Find the area of the inscribed circle [π = 3.14]
The area of a square is the same as the area of a square. Their perimeters are in the ratio
The circumference of a garden roller is 280 cm. How many revolutions does it make in moving 490 meters?
The speed of the car is 66 km/hour. If each wheel of the car is 140 cm in diameter, find the number of revolutions made by each wheel per minute.
The radius of a circle is 5 m. Find the circumference of the circle whose area is 49 times the area of the given circle.
What is the circumference of a circle of diameter 10 cm (Take π = 3.14)?
Ratio of the circumference of a circle to its diameter is denoted by symbol ______.
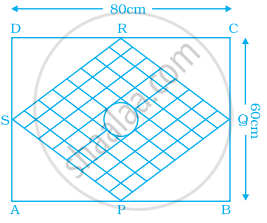
ABCD is a given rectangle with length as 80 cm and breadth as 60 cm. P, Q, R, S are the midpoints of sides AB, BC, CD, DA respectively. A circular rangoli of radius 10 cm is drawn at the centre as shown in the given figure. Find the area of shaded portion.