Advertisements
Advertisements
Question
The perimeter of a rhombus is 60 cm. If one of its diagonal us 18 cm long, find
(i) the length of the other diagonal, and
(ii) the area of the rhombus.
Solution
Perimeter of a rhombus = 4a (Here, a is the side of the rhombus)
⇒ `60=4a `
⇒ `a=15`
(i) Given:
One of the diagonals is 18 cm long
`d_1= 18cm`
Thus, we have:
Side= `1/2sqrt(d_1^2+d_2^2)`
⇒ `15=1/2sqrt(18^2+d_2^2)`
⇒`30=sqrt(18^2+d_2^2)`
Squaring both sides, we get:
⇒`900=18^2+d_2^2`
⇒`900=324+d_2^2`
⇒`d_2^2=576`
⇒`d_2^2=24cm`
(ii) Area of the rhombus=`1/2d_1xxd_2`
=`1/2xx18xx24`
=`216 cm^2`
APPEARS IN
RELATED QUESTIONS
A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire also used in making 5 diameters which divide the circle into 10 equal sectors as shown in Fig. Find:
(i) the total length of the silver wire required
(ii) the area of each sector of the brooch
The area of circle, inscribed in equilateral triangle is 154 cms2. Find the perimeter of
triangle.
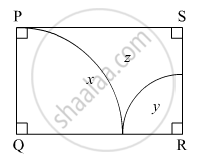
In the given figure,
\[\square\] PQRS is a rectangle. If PQ = 14 cm, QR = 21 cm, find the areas of the parts x, y, and z.
Find the perimeter of a semicircular protractor whose diameter is 14 cm.
The radii of two circles are 19 cm and 9 cm, Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.
A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the areas of the minor major segments.
A cylindrical bucket, whose base radius is 20 cm, is filled with water to a height of 25 cm. A heavy iron spherical ball of radius 10 cm is dropped to submerge completely in water in the bucket. Find the increase in the level of water.
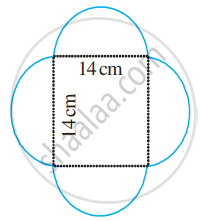
Find the perimeter of the given shape (Take π = `22/7`).
Circumference of a circle is always ______.
A circular pond is 17.5 m is of diameter. It is surrounded by a 2 m wide path. Find the cost of constructing the path at the rate of Rs 25 per m2.
