Advertisements
Advertisements
Question
A circular pond is 17.5 m is of diameter. It is surrounded by a 2 m wide path. Find the cost of constructing the path at the rate of Rs 25 per m2.
Solution
Radius of the circular pond r1 = `17.5/2` m = 8.75 m
Width of path = 2 m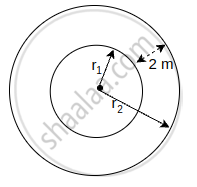
∴ Radius of the path including pond
r2 = 8.75 + 2 = 10.75 m
Area of path = `pi"r"_2^2 - pi"r"_1^2 = pi["r"_2^2 - "r"_1^2]`
Cost of constructing the path = Rs 25 `pi("r"_2^2 - "r"_1^2)`
∴ Required cost = Rs `25 xx 22/7 [(10.75)^2 - (8.75)^2]`
= `25 xx 22/7 [10.75 - 8.75][10.75 + 8.75]`
= `25 xx 22/7 xx 2 xx 19.5`
= `(50 xx 22 xx 19.5)/7`
= `(1100 xx 19.5)/7`
= `21450/7`
= Rs. 3064.29
Hence, the cost of constructing path is Rs 3064.29
RELATED QUESTIONS
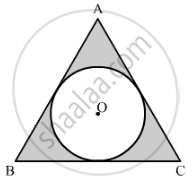
In Fig 4, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.[Use π=3.14 and √3=1.73]
If the circumference of a circular sheet is 154 m, find its radius. Also find the area of
the sheet. (Take `pi = 22/7`)
Choose the correct alternative answer for the following question.
The areas of two circles are in the ratio 4: 9. What is the ratio between their circumferences?
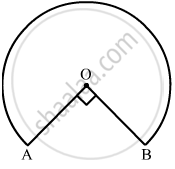
In the given figure, the shape of the top of a table is that of a sector of a circle with centre O and ∠AOB = 90°. If AO = OB = 42 cm,· then find the perimeter of the top of the table.
In a circle of radius 14 cm, an arc subtends an angle of 120° at the centre. If `sqrt(3) = 1.73` then the area of the segment of the circle is
A conical tent with a capacity of 600 m3 stands on a circular base of area 160 m2 Find in m2 the area of the canvas.
The sum of the radii of two circles is 10.5 cm and the difference of their circumferences is 13. 2 cm. Find the radii of the two circles.
A wheel of a car covers a distance of 3520 cm in 20 rotations. Find the radius of the wheel?
In covering a distance s metres, a circular wheel of radius r metres makes `s/(2πr)` revolutions. Is this statement true? Why?
