Advertisements
Advertisements
Question
A conical tent with a capacity of 600 m3 stands on a circular base of area 160 m2 Find in m2 the area of the canvas.
Solution
Area of the circular base = 160m2
`pir^2 = 160`
⇒ `r = sqrt((160 xx 7)/22)`
⇒ `r = sqrt(50.909)` = 7.134 m
Therefore , radius = 7.134 m
Capacity or Volume of the tent = 600m3
`1/3pir^2h = 600`
⇒ `1/3 xx 22/7 xx 7.13 xx 7.13 xx h = 600`
⇒ `h = (600 xx 3 xx 7)/(7.13 xx 7.13 xx 22)`
⇒ h = 11.265m
Therefore , vertical height = 11.265 m
We know slant height (l) =
l = `sqrt(r^2 + h^2)`
⇒ `l = sqrt(7.134^2 + 11.265^2)`
⇒ `l = sqrt(177.624) = 13.327`
Therefore , slant height = 13.327 m
The curved surface area = `pirl = 22/7 xx 7.134 xx 13.327` = 298.9m2
Hence , the area of the canvas = 298.9 m2
APPEARS IN
RELATED QUESTIONS
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
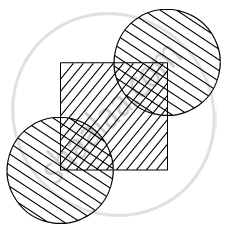
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find The area of sector
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that Perimeter of shaded region is 𝑟 (tan 𝜃 + sec 𝜃 +`(pitheta)/180`− 1)
Four equal circles each of radius a, touch each other. Show that area between them is `6/7a^2`
Choose the correct alternative answer for the following question.
The length of a chain used as the boundary of a semicircular park is 108 m. Find the area of the park.
The side of a square is 10 cm. Find the area of the inscribed circle [π = 3.14]
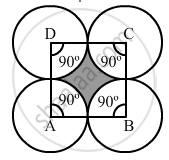
Four equal circles are described about the four corners of a square so that each touches two of the others, as shown in the figure. Find the area of the shaded region, if each side of the square measures 14 cm.
The radius of a circular garden is 100 m. There is a road 10 m wide, running all around it. Find the area of the road and the cost of levelling it at Rs 20 per m2. [Use π = 3.14]
In a circle of radius 14 cm, an arc subtends an angle of 120° at the centre. If `sqrt(3) = 1.73` then the area of the segment of the circle is
A bucket is raised from a well by means of a rope wound round a wheel of diameter 35 cm. If the bucket ascends in 2 minutes with a uniform speed of 1.1 m per sec, calculate the number of complete revolutions the wheel makes in raising the bucket.
Find the area and perimeter of the following semi-circle :
Diameter= 5.6 cm
Find the volume and the surface area of the spheres in the following :
Diameter= 6.3 cm
The circumference of a circular field is 308 m. Find is:
(i) Radius
(ii) Area.
In the given figure, the area of the shaded portion is 770 cm2. If the circumference of the outer circle is 132 cm, find the width of the shaded portion.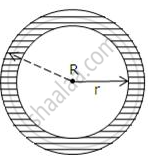
The radius of a circle is 5 m. Find the circumference of the circle whose area is 49 times the area of the given circle.
The sum of the circumference and diameter of a circle is 176 cm. Find the area of the circle.
The diameter of a wheel is 1.26 m. The distance traveled in 500 revolutions is ____________.
In reference to a circle the value of π is equal to ______.
A photograph of Billiard/Snooker table has dimensions as `1/10`th of its actual size as shown in the given figure:
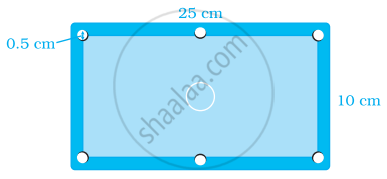
The portion excluding six holes each of diameter 0.5 cm needs to be polished at rate of ₹ 200 per m2. Find the cost of polishing.
