Advertisements
Advertisements
Question
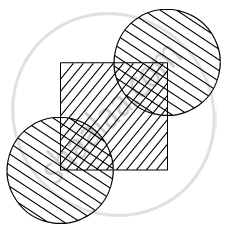
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
Solution
We have,
Side of square = 28 cm and radius of each circle = `28/2` cm
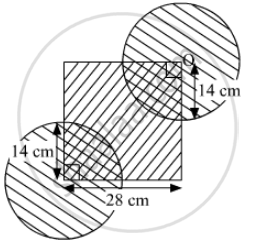
Area of the shaded region
= Area of the square + Area of the two circles − Area of the two quadrants
`= (28)^2 + 2 xx pi xx (28/2)^2 - 2 xx 1/4 xx pi xx (28/2)^2`
`= (28)^2 + 3/2 xx pi xx (28/2)^2`
`= (28)^2 (1 + 3/2 xx 22/7 xx 1/2 xx 1/2)`
`= (28)^2 xx 61/28`
`= 28 xx 61`
`= 1708 cm^2`
Therefore, the area of the shaded region is 1708 cm2
APPEARS IN
RELATED QUESTIONS
An arc of length 15 cm subtends an angle of 45° at the centre of a circle. Find in terms of 𝜋, radius of the circle.
The perimeter of a rhombus is 60 cm. If one of its diagonal us 18 cm long, find
(i) the length of the other diagonal, and
(ii) the area of the rhombus.
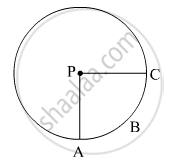
In the given figure, if A(P-ABC) = 154 cm2 radius of the circle is 14 cm, find
(1) `∠APC`
(2) l ( arc ABC) .
Choose the correct alternative answer for the following question.
The curved surface area of a cylinder is 440 cm 2 and its radius is 5 cm. Find its height.
A sector of 56°, cut out from a circle, contains 17.6 cm2. Find the radius of the circle.
The side of a square is 10 cm. Find the area of the inscribed circle [π = 3.14]
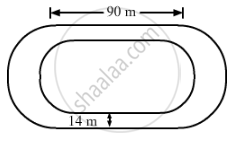
The inside perimeter of a running track shown in the figure is 400 m. The length of each of the straight portions is 90 m, and the ends are semicircles. If the track is 14 m wide everywhere, find the area of the track. Also, find the length of the outer boundary of the track.
The circumference of a garden roller is 280 cm. How many revolutions does it make in moving 490 meters?
Find the area of a circle whose circumference is 22 cm.
Find the circumference of a circle whose area is 81πcm2.
