Advertisements
Advertisements
Question
A photograph of Billiard/Snooker table has dimensions as `1/10`th of its actual size as shown in the given figure:
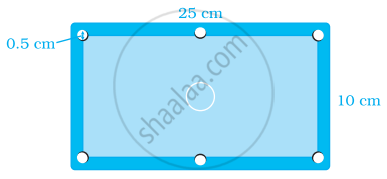
The portion excluding six holes each of diameter 0.5 cm needs to be polished at rate of ₹ 200 per m2. Find the cost of polishing.
Solution
Actual length = 25 × 10 = 250 cm
Actual breadth = 10 × 10 = 100 cm
Area of table = 250 × 100 = 25000 cm2
Radius of 1 hole = `0.5/2` = 0.25 cm
Area of 6 holes = 6 × πr2 = `6 xx 22/7 xx 0.25 xx 0.25` = 1.18 cm2
Area of portion excluding holes = 25000 – 1.18 = 24998.8 cm2
∴ Cost of polishing = ₹ `24999/10000 xx 200` = ₹ 500 (approx.)
APPEARS IN
RELATED QUESTIONS
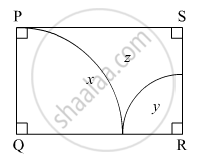
In the given figure,
\[\square\] PQRS is a rectangle. If PQ = 14 cm, QR = 21 cm, find the areas of the parts x, y, and z.
Find the length of the arc of a circle of diameter 42 cm which subtends an angle of 60° at the centre.
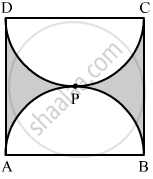
Find the perimeter of the shaded region in the figure, if ABCD is a square of side 14 cm and APB and CPD are semicircles.
A copper wire when bent in the form of a square encloses an area of 484 cm2. The same wire is not bent in the form of a circle. Find the area enclosed by the circle.
Three equal circles, each of radius 6 cm, touch one another as shown in the figure. Find the area of enclosed between them.

The perimeter of a circular field is 242 m. The area of the field is
A hollow metallic cylindrical tube has an internal radius of 3.5 cm and height 21 cm. The thickness of the metal tube is 0.5 cm. The tube is melted and cast into a right circular cone of height 7 cm. Find the radius of the cone, correct to one decimal place.
A metal wire, when bent in the form of an equilateral triangle of largest area, encloses an area of 484 `sqrt3` cm2. If the same wire is bent into the form of a circle of largest area, find the area of this circle.
Find the area of a circular field that has a circumference of 396m.
The area between the circumference of two concentric circles is 2464cm2. If the inner circle has a circumference of 132cm, calculate the radius of the outer circle.
