Advertisements
Advertisements
Question
In figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.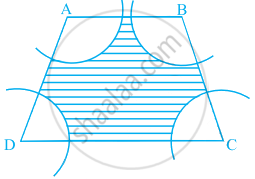
Solution
AB = 18 cm,
DC = 32 cm
Distance between AB and DC = Height = 14 cm
Now, Area of the trapezium
= `1/2 xx "Sum of parallel sides" xx "Height"`
= `1/2 xx 18 + 32 xx 14`
= 350 cm2
As AB ∥ DC,
∴ ∠A + ∠D = 180°
And ∠B + ∠C = 180°
Also, radius of each arc = 7 cm
Therefore,
Area of the sector with central angle A = `1/2 xx (∠"A")/180^circ xx π xx "r"^2`
Area of the sector with central angle D = `1/2 xx (∠"D")/180^circ xx π xx "r"^2`
Area of the sector with central angle B = `1/2 xx (∠"B")/180^circ xx π xx "r"^2`
Area of the sector with central angle C = `1/2 xx (∠"C")/180^circ xx π xx "r"^2`
Total area of the sectors,
= `(∠"A")/360^circ xx pi xx "r"^2 + (∠"D")/360^circ xx pi xx "r"^2 + (∠"B")/360^circ xx pi xx "r"^2 + (∠"C")/360^circ xx pi xx "r"^2`
= `((∠"A" + ∠"D")/360^circ xx pi xx "r"^2) + ((∠"B" + ∠"C")/360^circ xx pi xx "r"^2)`
= `(180^circ/360^circ xx 22/7 xx 49) + (180^circ/360^circ xx 22/7 xx 49)`
= 77 + 77
= 154
∴ Area of shaded region
= Area of trapezium – (Total area of sectors)
= 350 – 154
= 196 cm2
Hence, the required area of shaded region is 196 cm2.
APPEARS IN
RELATED QUESTIONS
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding:
Major sector [Use π = 3.14]
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
The diameter of a sphere is 6 cm, Find the total surface area of the sphere. (π = 3.14)
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
If the area of a circle is numerically equal to twice its circumference, then the diameter of the circle is ____________.
Find the area of a sector of a circle of radius 28 cm and central angle 45°.
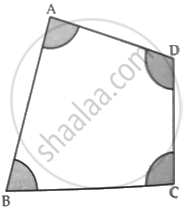
In the given figure, arcs have been drawn of radius 7 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
Find the area of the unshaded region shown in the given figure.