Advertisements
Advertisements
प्रश्न
In figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.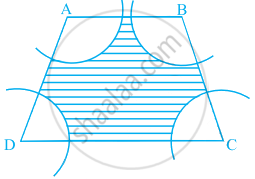
उत्तर
AB = 18 cm,
DC = 32 cm
Distance between AB and DC = Height = 14 cm
Now, Area of the trapezium
= `1/2 xx "Sum of parallel sides" xx "Height"`
= `1/2 xx 18 + 32 xx 14`
= 350 cm2
As AB ∥ DC,
∴ ∠A + ∠D = 180°
And ∠B + ∠C = 180°
Also, radius of each arc = 7 cm
Therefore,
Area of the sector with central angle A = `1/2 xx (∠"A")/180^circ xx π xx "r"^2`
Area of the sector with central angle D = `1/2 xx (∠"D")/180^circ xx π xx "r"^2`
Area of the sector with central angle B = `1/2 xx (∠"B")/180^circ xx π xx "r"^2`
Area of the sector with central angle C = `1/2 xx (∠"C")/180^circ xx π xx "r"^2`
Total area of the sectors,
= `(∠"A")/360^circ xx pi xx "r"^2 + (∠"D")/360^circ xx pi xx "r"^2 + (∠"B")/360^circ xx pi xx "r"^2 + (∠"C")/360^circ xx pi xx "r"^2`
= `((∠"A" + ∠"D")/360^circ xx pi xx "r"^2) + ((∠"B" + ∠"C")/360^circ xx pi xx "r"^2)`
= `(180^circ/360^circ xx 22/7 xx 49) + (180^circ/360^circ xx 22/7 xx 49)`
= 77 + 77
= 154
∴ Area of shaded region
= Area of trapezium – (Total area of sectors)
= 350 – 154
= 196 cm2
Hence, the required area of shaded region is 196 cm2.
APPEARS IN
संबंधित प्रश्न
In the following figure, if m(are DXE) = 90° and m(are AYC) = 30°. Find ∠DBE.

In Fig. 3, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding:
Major sector [Use π = 3.14]
In the given figure, A is the center of the circle. ∠ABC = 45° and AC = 7√2 cm. Find the area of segment BXC.
In the given figure, if O is the center of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of the shaded region is 114 cm2, find the radius of the circle. \[\pi\] = 3.14)

A chord of length 6 cm is at a distance of 7.2 cm from the centre of a circle. Another chord of the same circle is of length 14.4 cm. Find its distance from the centre.
A car has two wipers that do not overlap. Each wiper has a blade of length 21 cm sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades. `("Take" π =22/7)`
Find the area of the minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 60°.
A piece of wire 20 cm long is bent into the form of an arc of a circle subtending an angle of 60° at its centre. Find the radius of the circle.
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
