Advertisements
Advertisements
प्रश्न
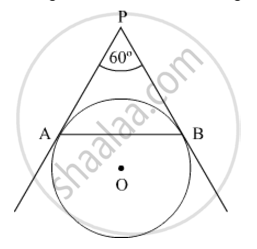
In Fig. 3, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.
उत्तर
PA and PB are tangents drawn to the given circle from an external point P.
It is known that the lengths of the tangents drawn from an external point to a circle are equal.
∴ PA = PB
In ∆PAB, sides PA and PB are of the same length.
Hence, ∆PAB is isosceles, with PA = PB and ∠PAB = ∠PBA = x (say).
It is given that
∠APB = 60°
We know that the sum of the angles of a triangle is 180°
In ∆PAB,
∠PAB + ∠PBA + ∠APB = 180°
∴ x + x + 60° = 180°
⇒ 2x = 120°
⇒ x = 60°
Thus,
∠PAB = ∠PBA = ∠APB = 60°
Since all angles of ∆PAB are of the same measure, ∆PAB is equilateral, with AP = BP = AB.
It is given that
AP = 5 cm
∴ AB = AP = 5 cm
Thus, the length of the chord AB is 5 cm.
APPEARS IN
संबंधित प्रश्न
A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. [Use π = 3.14 and `sqrt3 = 1.73`]
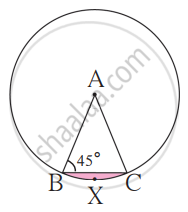
In the given figure, A is the center of the circle. ∠ABC = 45° and AC = 7√2 cm. Find the area of segment BXC.
Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
The length of the minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6 : 05 am and 6 : 40 am.
The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
The radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
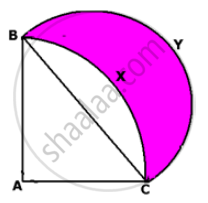
Find the area of the shaded region where ABC is a quadrant of radius 5cm and a semicircle is drawn with BC as diameter.
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
In the given figure, arcs have been drawn of radius 7 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.