Advertisements
Advertisements
प्रश्न
The length of the minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6 : 05 am and 6 : 40 am.
उत्तर
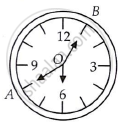
We know that, in 60 mins, minute hand revolving = 360°
In 1 min, minute hand revolving = `360^circ/60^circ`
∴ In (6 : 05 am to 6 : 40 am) = 35 mins,
minute hand revolving = `360^circ/60 xx 35` = (6 × 35)°
Given that, length of minute hand (r) = 5 cm
∴ Area of sector AOBA with angle ∠O
= `(π"r"^2)/360^circ xx ∠"O"`
= `22/7 xx (5)^2/360^circ xx (6 xx 35)^circ`
= `22/7 xx (5 xx 5)/360^circ xx (6 xx 35)^circ`
= `(22 xx 5 xx 5 xx 5)/60^circ`
= `(22 xx 5 xx 5)/12`
= `(11 xx 5 xx 5)/6`
= `275/6`
= `45 5/6 "cm"^2`
Hence, the required area swept by the minute hand is `45 5/6 "cm"^2`.
संबंधित प्रश्न
A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. [Use π = 3.14 and `sqrt3 = 1.73` ]
In a circle of radius 35 cm, an arc subtends an angle of 72° at the centre. Find the length of arc and area of sector
A sector is cut-off from a circle of radius 21 cm the angle of sector is 120°. Find the length of its arc and its area.
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`
In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
In figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle. Is the area of the outer square four times the area of the inner square? Give reasons for your answer.
Find the area of the minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 60°.
In figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.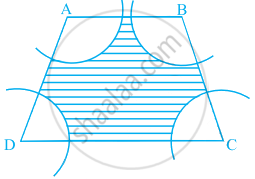
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
