Advertisements
Advertisements
प्रश्न
The length of the minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6 : 05 am and 6 : 40 am.
उत्तर
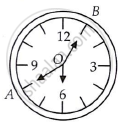
We know that, in 60 mins, minute hand revolving = 360°
In 1 min, minute hand revolving = `360^circ/60^circ`
∴ In (6 : 05 am to 6 : 40 am) = 35 mins,
minute hand revolving = `360^circ/60 xx 35` = (6 × 35)°
Given that, length of minute hand (r) = 5 cm
∴ Area of sector AOBA with angle ∠O
= `(π"r"^2)/360^circ xx ∠"O"`
= `22/7 xx (5)^2/360^circ xx (6 xx 35)^circ`
= `22/7 xx (5 xx 5)/360^circ xx (6 xx 35)^circ`
= `(22 xx 5 xx 5 xx 5)/60^circ`
= `(22 xx 5 xx 5)/12`
= `(11 xx 5 xx 5)/6`
= `275/6`
= `45 5/6 "cm"^2`
Hence, the required area swept by the minute hand is `45 5/6 "cm"^2`.
संबंधित प्रश्न
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
The area of sector of circle of radius 5cm is 5𝜋 cm2. Find the angle contained by the sector.
In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.
Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed?
The diameter of a sphere is 6 cm, Find the total surface area of the sphere. (π = 3.14)
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
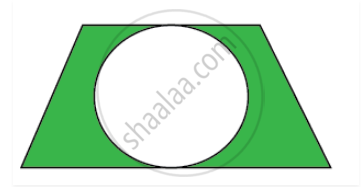
In the given figure, a circle is inscribed in a trapezium of height 14 cm and lengths of parallel sides are equal to 25 cm and 40 cm. What is the area of the shaded region?
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
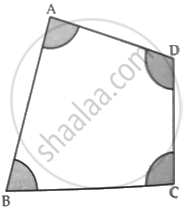
In the given figure, arcs have been drawn of radius 7 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.