Advertisements
Advertisements
प्रश्न
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
उत्तर
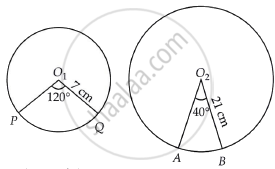
Let the lengths of the corresponding arcs be l1 and l2.
Given that, radius of sector PO1QP = 7 cm
And radius of sector AO2BA = 21 cm
Central angle of the sector PO1QP (θ1) = 120°
And central angle of the sector AO2BA (θ2) = 40°
∴ Area of the sector with central angle O1
= `(pi"r"^2)/360^circ xx θ_1`
= `(pi(7)^2)/360^circ xx 120^circ`
= `22/7 xx (7 xx 7)/360^circ xx 120^circ`
= `(22 xx 7)/3`
= `154/3 "cm"^2`
And area of the sector with central angle O2
= `(pi"r"^2)/360^circ xx θ_2`
= `(pi(21)^2)/360^circ xx 40^circ`
= `22/7 xx (21 xx 21)/360^circ xx 40^circ`
= `(22 xx 3 xx 21)/9`
= 22 × 7
= 154 cm2
Now, corresponding arc length of the sector PO1QP
= `θ_1/360^circ xx 2pi"r"`
= `120^circ/360^circ xx 2 xx 22/7 xx 7`
= `44/3 "cm"`
And corresponding arc length of the sector AO2BA
= `θ_2/360^circ xx 2pi"r"`
= `40^circ/360^circ xx 2 xx 22/7 xx 21`
= `44/3 "cm"`
Hence, we observe that arc lengths of two sectors of two different circles may be equal but their area need not be equal.
APPEARS IN
संबंधित प्रश्न
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60° [Use `pi = 22/7`]
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding:
Major sector [Use π = 3.14]
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) The length of the arc
(ii) Area of the sector formed by the arc
(iii) Area of the segment forced by the corresponding chord
[use Π = 22/7]
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
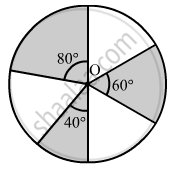
In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region.
Find the area of the sector whose arc length and radius are 8 cm and 3 cm respectively.
A car has two wipers that do not overlap. Each wiper has a blade of length 21 cm sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades. `("Take" π =22/7)`
If `theta` is the angle in degrees of a sector of a circle of radius V, then area of the sector is ____________.
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
In figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.