Advertisements
Advertisements
प्रश्न
Find the area of the shaded region given in figure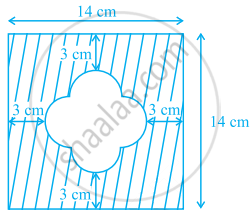
उत्तर
ABCD is a square of side 14 cm.
Join JK, KL, LM and MJ.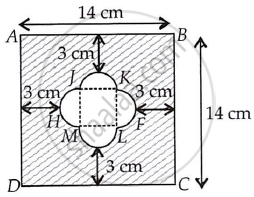
There are four equal semi-circles and JKLM formed a square.
∴ FH = 14 – (3 + 3) = 8 cm
So, the side of square JKLM is 4 cm and radius of semi-circle of both ends are 2 cm each.
∴ Area of square JKLM = (4)2 = 16 cm2
Area of semi-circle HJM = `(π"r"^2)/2`
= `(π xx (2)^2)/2`
= 2π cm2
∴ Area of four semi-circles
= 4 × 2π
= 8π cm2
Now, area of square ABCD = (14)2 cm2 = 196 cm2
∴ Area of shaded region = Area of square
ABCD – [Area of four semi-circles + Area of square JKLM]
= 196 – [8π + 16]
= 196 – 16 – 8π
= (180 – 8π) cm2
Hence, the required area of the shaded region is (180 – 8π) cm2.
APPEARS IN
संबंधित प्रश्न
The parallel sides of trapezium are 12 cm and 9cm and the distance between them is 8 cm. Find the area of the trapezium.
Three equal circles, each of radius 6 cm, touch one another as shown in the figure. Find the area of enclosed between them.

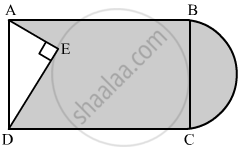
In the given figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π = 3.14]
The perimeter of a sector of a circle of radius 5.6 cm is 27.2 cm. Find the area of the sector.
Find the circumference of the circle whose area is 81π cm 2.
Construct an angle PQR = 45°. Mark a point S on QR such that QS = 4.5 cm. Construct a circle to touch PQ at Q and also to pass through S.
The speed of a car is 66km per hour. If each wheel of the car is 140cm in diameter, find the number if revolution made by each wheel per minute.
A wire of length 1320 cm is made into circular frames of radius 7 cm each. How many frames can be made?
A Rose garden is in the form of circle of radius 63 m. The gardener wants to fence it at the rate of ₹ 150 per metre. Find the cost of fencing?
If the circumference of a circle is 82π, then the value of ‘r’ is
