Advertisements
Advertisements
प्रश्न
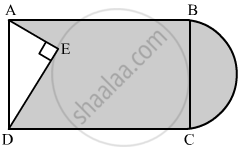
In the given figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π = 3.14]
उत्तर
In right triangle AED
AD2 = AE2 + DE2
= (9)2 + (12)2
= 81 + 144
= 225
∴ AD2 = 225
⇒ AD = 15 cm
We know that the opposite sides of a rectangle are equal
AD = BC = 15 cm
= Area of the shaded region = Area of rectangle − Area of triangle AED + Area of semicircle
= 300 - 54 + 88.31
= 334. 31 cm2
Hence, the area of shaded region is 334.31 cm2
APPEARS IN
संबंधित प्रश्न
Find the circumference of a circle whose area is 301.84 cm2.
The area of a minor sector of a circle is 3.85 cm2 and the measure of its central angle is 36°. Find the radius of the circle.
Choose the correct alternative answer for the following question.
The curved surface area of a cylinder is 440 cm 2 and its radius is 5 cm. Find its height.
In a circle of radius 10.5 cm, the minor arc is one-fifth of the major arc. Find the area of the sector corresponding to the major arc.
The wheels of a car make 2500 revolutions in covering a distance of 4.95 km. Find the diameter of a wheel.
The perimeter of a circular field is 242 m. The area of the field is
Find the area of the circle if its circumfence is 88 cm.
The radii of two circles are 48 cm and 13 cm. Find the area of the circle which has its circumference equal to the difference of the circumferences of the given two circles.
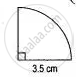
In the adjoining figure, the radius is 3.5 cm. Find:
(i) The area of the quarter of the circle correct to one decimal place.
(ii) The perimeter of the quarter of the circle correct to one decimal place. ( Take π =
The cost of fencing a circular race course at the rate of ₹ 8 per metre is ₹ 2112. Find the diameter of the race course
