Advertisements
Advertisements
प्रश्न
In the given figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π = 3.14]
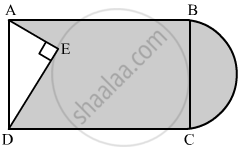
उत्तर
In right triangle AED
AD2 = AE2 + DE2
= (9)2 + (12)2
= 81 + 144
= 225
∴ AD2 = 225
⇒ AD = 15 cm
We know that the opposite sides of a rectangle are equal
AD = BC = 15 cm
= Area of the shaded region = Area of rectangle − Area of triangle AED + Area of semicircle
`="AB"xx"BC" - 1/2xx"AE"xx"DE"+1/2pi("BC"/2)^2`
`= 20xx15-1/2xx9xx12+1/2xx3.14(15/2) `^2
= 300 - 54 + 88.31
= 334. 31 cm2
Hence, the area of shaded region is 334.31 cm2
APPEARS IN
संबंधित प्रश्न
A race track is in the form of a ring whose inner circumference is 352 m, and the outer circumference is 396 m. Find the width of the track.
An arc of length 15 cm subtends an angle of 45° at the centre of a circle. Find in terms of 𝜋, radius of the circle.
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find Length of arc
The circumferences of two circles are in the ratio 2: 3. What is the ratio between their areas?
Find the area of a circular field that has a circumference of 396 m.
Find the diameter of the sphere for the following :
Surface Area = `576pi`cm2
A wheel has a diameter of 84 cm. Find how many completer revolutions must it make to cover 3.168 km.
Construct the circumcircle of the ABC when BC = 6 cm, B = 55° and C = 70°.
The diameter of the wheel of a cart is 1.05 m. How much distance will the cart cover in 1000 rotations of the wheel?
Find the radius of a circle whose circumference is equal to the sum of the circumferences of two circles of radii 15 cm and 18 cm.
