Advertisements
Advertisements
प्रश्न
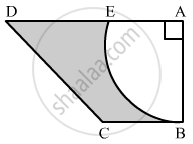
In the given figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region.
उत्तर
Area of trapezium `=1/2("AD" + "BC")xx"AB"`
`=>24.5 = 1/2(10+4)xx"AB"`
⇒ AB = 3.5 cm
Area of shaded region = Area of trapezium ABCD − Area of quadrant ABE
`= 24.5 - 1/4pi("AB")^2`
`= 24.5-1/4xx22/7(3.5)^2`
= 24.5- 9.625
= 14.875 cm2
Hence, the area of shaded region is 14.875 cm2
APPEARS IN
संबंधित प्रश्न
All the vertices of a rhombus lie on a circle. Find the area of the rhombus, if the area of the circle is 1256 cm2. (Use π = 3.14)
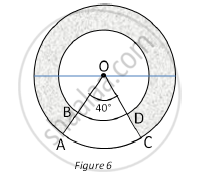
In Fig. 6, find the area of the shaded region, enclosed between two concentric circles of radii 7 cm and 14 cm where ∠AOC = 40°. (use `pi = 22/7`)
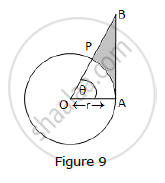
In Fig. 9, is shown a sector OAP of a circle with centre O, containing ∠θ. AB is perpendicular to the radius OQ and meets OP produced at B. Prove that the perimeter of shaded region is
`r[tantheta+sectheta+(pitheta)/180-1]`
A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also find the costs of the rope, if it cost ₹ 4 per meter. (Take `pi = 22/7`)
The area of circle, inscribed in equilateral triangle is 154 cms2. Find the perimeter of
triangle.
The sum of the radii of two circles is 7 cm, and the difference of their circumferences is 8 cm. Find the circumference of the circles.
A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the areas of the minor major segments.
A 4.2 m wide road surrounds a circular plot whose circumference is 176 m. Find the cost of paving the road at Rs 75 m 2.
Find the area and perimeter of the circles with following: Diameter = 35cm
Find the perimeter of the given shape (Take π = `22/7`).