Advertisements
Advertisements
Question
In the given figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region.
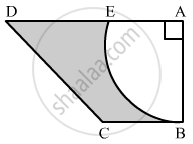
Solution
Area of trapezium `=1/2("AD" + "BC")xx"AB"`
`=>24.5 = 1/2(10+4)xx"AB"`
⇒ AB = 3.5 cm
Area of shaded region = Area of trapezium ABCD − Area of quadrant ABE
`= 24.5 - 1/4pi("AB")^2`
`= 24.5-1/4xx22/7(3.5)^2`
= 24.5- 9.625
= 14.875 cm2
Hence, the area of shaded region is 14.875 cm2
APPEARS IN
RELATED QUESTIONS
The radius of a circle is 7 cm. find the circumference of the circle.
The short and long hands of a clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 2 days. (Take π = 22/7)
Find the perimeter of a semicircular protractor whose diameter is 14 cm.
The sum of the radii of two circles is 7 cm, and the difference of their circumferences is 8 cm. Find the circumference of the circles.
Find the total surface area and volume of a hemisphere whose radius is 10 cm.
Complete the table below.
| Radius (r) | Diameter (d) | Circumference (c) |
| ...... | 28 cm | ...... |
The circumference o a garden roller is 280cm. How many revolutions does it make in moving 490m?
The area between the circumference of two concentric circles is 2464cm2. If the inner circle has a circumference of 132cm, calculate the radius of the outer circle.
Find the circumference of the circles whose radii are given below.
91 mm
The cost of fencing a circular race course at the rate of ₹ 8 per metre is ₹ 2112. Find the diameter of the race course
