Advertisements
Advertisements
प्रश्न
If three circles of radius a each, are drawn such that each touches the other two, prove that the area included between them is equal to `4/25"a"^2`.
उत्तर
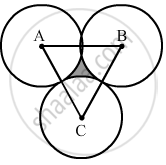
When three circles touch each other, their centres form an equilateral triangle, with each side being 2a.
Area of the triangle`=sqrt(3)/4xx2"a"xx2"a" = sqrt(3)"a"^2`
Total area of the three sectors of circles `=3xx60/360xx22/7xx"a"^2 = 1/2xx22/7 "a"^2 = 11/7"a" ^2`
Area of the region between the circles = Area of the triangle - Area of three sectors
`=(sqrt(3)-11/7)"a"^2`
= (1.73 - 1.57)a2
= 0.16 a2
= 0.16 a2
`=4/25"a"^2 `
APPEARS IN
संबंधित प्रश्न
The adjacent sides of a parallelogram are 32 cm and 24 cm. If the distance between the longer sides is 17.4 cm, find the distance between the shorter sides.
A chord of a circle of radius 20 cm sub tends an angle of 900 at the centre . Find the area of the corresponding major segment of the circle
( Use \[\pi = 3 . 14\])
In the following figure find the area of the shaded region. (Use π = 3.14)
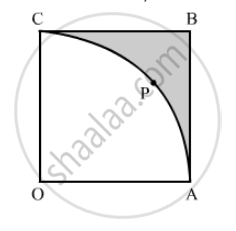
In the following figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. (Use π = 22/7)
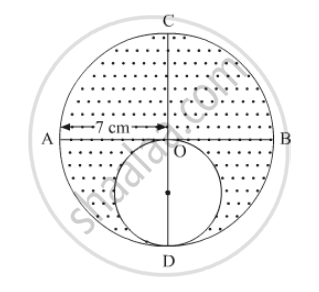
In the following figure, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
The minute hand of a clock is 15 cm long. Calculate the area swept by it in 20 minutes.
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made.
The given figures show a rectangle ABCD inscribed in a circle as shown alongside.
If AB = 28 cm and BC = 21 cm, find the area of the shaded portion of the given figure.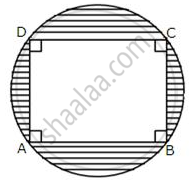
Find the area of a ring-shaped region enclosed between two concentric circles of radii 20 cm and 15 cm.
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
