Advertisements
Advertisements
प्रश्न
If three circles of radius a each, are drawn such that each touches the other two, prove that the area included between them is equal to `4/25"a"^2`.
उत्तर
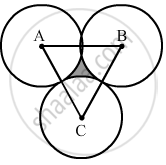
When three circles touch each other, their centres form an equilateral triangle, with each side being 2a.
Area of the triangle`=sqrt(3)/4xx2"a"xx2"a" = sqrt(3)"a"^2`
Total area of the three sectors of circles `=3xx60/360xx22/7xx"a"^2 = 1/2xx22/7 "a"^2 = 11/7"a" ^2`
Area of the region between the circles = Area of the triangle - Area of three sectors
`=(sqrt(3)-11/7)"a"^2`
= (1.73 - 1.57)a2
= 0.16 a2
= 0.16 a2
`=4/25"a"^2 `
APPEARS IN
संबंधित प्रश्न
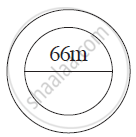
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
A rectangular park 358 m long and 18 m wide is to be covered with grass, leaving 2.5 m uncovered all around it. Find the area to be laid with grass.
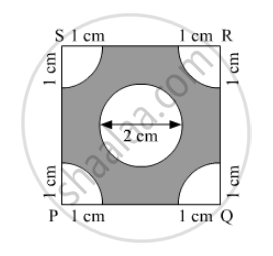
In the following figure, PQRS is a square of side 4 cm. Find the area of the shaded square.
If a chord of a circle of radius 28 cm makes an angle of 90 ° at the centre, then the area of the major segment is
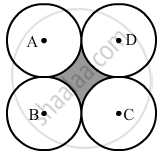
Four equal circles, each of radius 5 cm, touch each other, as shown in the figure. Find the area included between them.
A wire, when bent in the form of a square; encloses an area of 196 cm2. If the same wire is bent to form a circle; find the area of the circle.
Find the area enclosed between two concentric circles of radii 6.3cm and 8.4cm. A third concentric circle is drawn outside the 8.4cm circle. So that the area enclosed between it and the 8.4cm circle is the same as that between the two inner circles. Find the radii of the third circle correct to two decimal places.
Find the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm.
Find the area of the shaded region:
If the radius of a semi-circular protractor is 7cm, then its perimeter is ______.
