Advertisements
Advertisements
प्रश्न
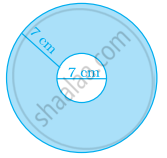
Find the area of the shaded region:
उत्तर
Let radius of smaller circle be r and bigger circle be R
From the figure r = `7/2` cm and R = `7/2 + 7 = 21/2`cm
∴ Area of shaded region = Area of bigger circle – Area of smaller circle
= πR2 – πr2
= π(R2 – r2)
= `π(21/2 xx 21/2 - 7/2 xx 7/2)`
= `π(441/4 - 49/4)`
= `22/7 xx 392/4`
= 308 cm2
Hence, the area of shaded region is 308 cm2.
APPEARS IN
संबंधित प्रश्न
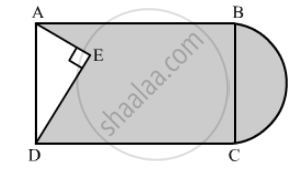
In the following figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π =]`22/7` [CBSE 2014]
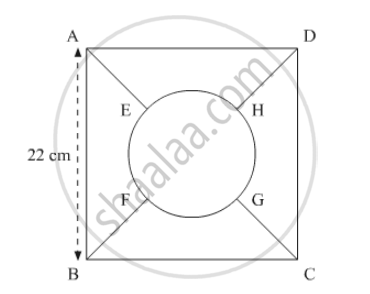
In the following figure, the square ABCD is divided into five equal parts, all having same area. The central part is circular and the ines AE, GC, BF and HD lie along the diagonals AC and BD of the square. If AB = 22 cm, find:
the circumference of the central part.
ABCDEF is a regular hexagon with centre O (in the following figure). If the area of triangle OAB is 9 cm2, find the area of : (i) the hexagon and (ii) the circle in which the haxagon is incribed.
Find the area of sector of circle of radius 21 cm and central angle 1200.
If the numerical value of the area of a circle is equal to the numerical value of its circumference , find its radius.
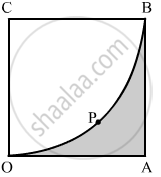
In the given figure, OABC is a square of side 7 cm. If COPB is a quadrant of a circle with centre C find the area of the shaded region.
The area of a circle is 98.56 cm2. Find its circumference.
A horse is tethered to one corner of a field which is in the shape of an equilateral triangle of side 12 m. If the length of the rope is 7 m, find the area of the field which the horse cannot graze. Write the answer correct to 2 places of decimal.
The length of an arc of the sector of angle θ° of a circle with radius R is
Find the area enclosed between two concentric circles of radii 6.3cm and 8.4cm. A third concentric circle is drawn outside the 8.4cm circle. So that the area enclosed between it and the 8.4cm circle is the same as that between the two inner circles. Find the radii of the third circle correct to two decimal places.
