Advertisements
Advertisements
Question
Find the area of the shaded region:
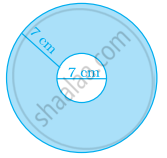
Solution
Let radius of smaller circle be r and bigger circle be R
From the figure r = `7/2` cm and R = `7/2 + 7 = 21/2`cm
∴ Area of shaded region = Area of bigger circle – Area of smaller circle
= πR2 – πr2
= π(R2 – r2)
= `π(21/2 xx 21/2 - 7/2 xx 7/2)`
= `π(441/4 - 49/4)`
= `22/7 xx 392/4`
= 308 cm2
Hence, the area of shaded region is 308 cm2.
APPEARS IN
RELATED QUESTIONS
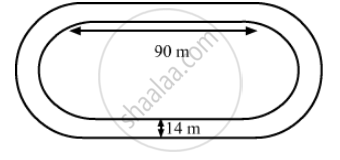
The inside perimeter of a running track (shown in the following figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide. find the area of the track. Also find the length of the outer running track.
If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
How many revolutions a circular wheel of radius r metres makes in covering a distance of s metres?
The ratio of the outer and inner perimeters of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is
The diameter of the wheels of a bus is 140 cm. How many revolutions per minute do the wheels make when the bus is moving at a speed of 72.6 km per hour?
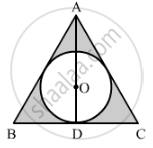
In the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.
[Use `sqrt(3)= 1.73, pi = 3.14]`
The length of the minute hand of a clock is 21 cm. The area swept by the minute hand in 10 minutes is
Two circles touch externally. The sum of their areas is 130π sq. cm and the distance between their centers is 14 cm. Find the radii of the circles.
Find the radius and area of a circle, whose circumference is :
(i) 132 cm
(ii) 22 m
Find the area of a circle of radius 30 cm (use π = 3.14).
