Advertisements
Advertisements
Question
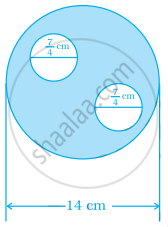
Find the area of the shaded region:
Solution
∵ Diameter of complete circle = 14 cm
∴ Radius = `14/2` = 7 cm .....`[∵ "Radius" = "Diameter"/2]`
So, area of complete circle = πr2 = `22/7 xx 7 xx 7` = 154 cm2
∵ Diameter of small circle = `7/4`cm
∴ Radius = `7/(4 xx 2) = 7/8`cm
∴ Area of two small circles = 2 × πr2
= `2 xx 22/7 xx 7/8 xx 7/8`
= `77/16`cm2
∴ Area of shaded region = Area of complete circle – Area of two small circles
= `154 - 77/16`
= `(154 xx 16 - 77)/16` ......[Taking LCM]
= `(2464 - 77)/16`
= `2387/16`
= `149 3/16` cm2
Hence, the area of shaded region is `149 3/16`cm2.
APPEARS IN
RELATED QUESTIONS
A calf is tied with a rope of length 6 m at the corner of a square grassy lawn of side 20 m . If the length of the rope is increased by 5.5 m , find the increase in area of the grassy lawn in which the calf can graze .
The area of a circle is 220 cm2. The area of ta square inscribed in it is
If the circumference of a circle increases from 4π to 8π, then its area is
A rope by which a cow is tethered is increased from 16 m to 23 m. How much additional ground does it have now graze?
ABCD is a field in the shape of a trapezium, AD || BC, ∠ABC = 90° and ∠ADC = 60°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m. Find the following:
- total area of the four sectors,
- area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.

A circular disc of radius 6 cm is divided into three sectors with central angles 90°,120° and 150°. What part of the whole circle is the sector with central angle 150°? Also, calculate the ratio of the areas of the three sectors.
The area of a sector of a circle with radius r, making an angle of x° at the centre is
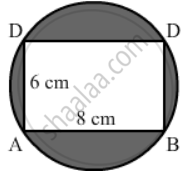
In the given figure, ABCD is a rectangle inscribed in a circle having length 8 cm and breadth 6 cm. If π = 3.14, then the area of the shaded region is:
A circle of the largest area is cut from a rectangular piece of cardboard with dimensions 55 cm and 42 cm. Find the ratio between the area of the circle cut and the area of the remaining card-board.
Two circles touch externally. The sum of their areas is 130π sq. cm and the distance between their centers is 14 cm. Find the radii of the circles.
