Advertisements
Advertisements
Question
A calf is tied with a rope of length 6 m at the corner of a square grassy lawn of side 20 m . If the length of the rope is increased by 5.5 m , find the increase in area of the grassy lawn in which the calf can graze .
Solution
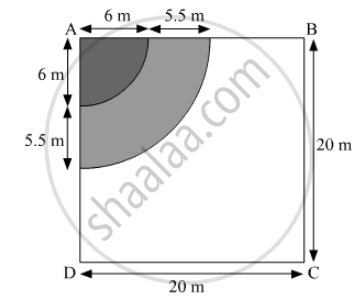
The area grazed by the calf is in the form of a quadrant of a circle with radius 6 m.
Area grazed by the calf with rope 6 m=`1/4pi(6)^2`
`=28.28 m^2`
When the rope length is increased then total rope length = 6 + 5.5 m = 11.5 m
Area covered by the calf for grazing with rope `11.5 m=1/4pi(11.5)^2`
`=103.91 m^2`
Hence, increase in area of grassy lawn that is grazed = 103.91 − 28.28 = 75.63 m2
APPEARS IN
RELATED QUESTIONS
The cost of harvesting a square field at ₹ 900 per hectare is ₹ 8100. Find the cost of putting a fence around it at ₹ 18 per meter.
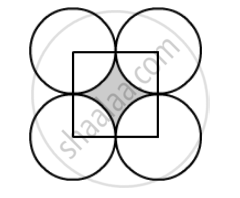
The diameter of a coin is 1 cm (in the following figure). If four such coins be placed on a table so that the rim of each touches that of the other two, find the area of the shaded region (Take π = 3.1416).
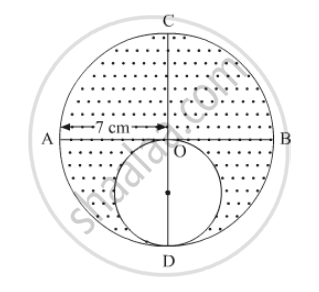
In the following figure, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square .
If the area of a sector of a circle is `5/18` of the area of the circle, then the sector angle is equal to
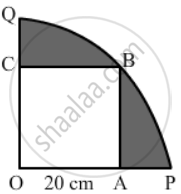
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
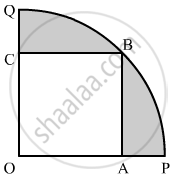
In the given figure, a square OABC has been inscribed in the quadrant OPBQ. If OA = 20 cm, then the area of the shaded region is
The minute hand of a clock is 12 cm long. Find the area of the face of the clock described by the minute hand in 35 minutes.
The diameters of two circles are 32 cm and 24 cm. Find the radius of the circle having its area equal to the sum of the areas of the two given circles.
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is ______.
