Advertisements
Advertisements
Question
A circular disc of radius 6 cm is divided into three sectors with central angles 90°,120° and 150°. What part of the whole circle is the sector with central angle 150°? Also, calculate the ratio of the areas of the three sectors.
Solution
Area of sector having central angle 150° `=150^circ/360^circ(6)^2= 5/12xx"Area of circular disc"`
Now, Area of sector having central angle 90° : Area of sector having central angle 120° : Area of sector having central angle 150°
`= 90^circ/360^circ pi (6)^2 : 120^circ/360^circ(6)^2: 150/360pi(6)^2`
`= 1/4 : 1/3 : 5/12`
= 3 : 4 : 5
APPEARS IN
RELATED QUESTIONS
Find the area of the following circles, given that radius = 5 cm.
The base of an isosceles triangle measures 80 cm and its area is 2 `360 . cm^2` Find the perimeter of the triangle.
A calf is tied with a rope of length 6 m at the corner of a square grassy lawn of side 20 m . If the length of the rope is increased by 5.5 m , find the increase in area of the grassy lawn in which the calf can graze .
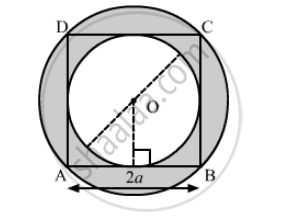
In the following figure, ABCD is a square of side 2a, Find the ratio between
(i) the circumferences
(ii) the areas of the in circle and the circum-circle of the square.
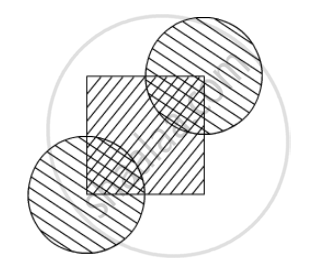
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
The radius of a wheel is 0.25 m. The number of revolutions it will make to travel a distance of 11 km will be
If π is taken as `22/7` the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution, is
The area of a circle is 98.56 cm2. Find its circumference.
Two circles touch externally. The sum of their areas is 130π sq. cm and the distance between their centers is 14 cm. Find the radii of the circles.
The ratio of the area of a circle to the area of its semicircle is
