Advertisements
Advertisements
Question
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
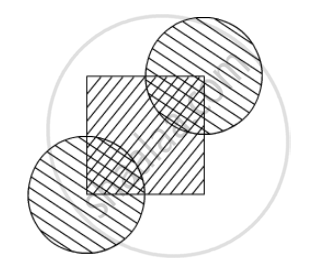
Solution
We have,
Side of square = 28 cm and radius of each circle = \[\frac{28}{2}\] cm
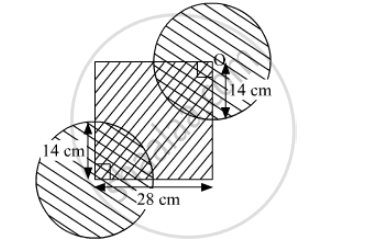
Area of the shaded region
= Area of the square + Area of the two circles − Area of the two quadrants
\[= \left( 28 \right)^2 + 2 \times \pi \times \left( \frac{28}{2} \right)^2 - 2 \times \frac{1}{4} \times \pi \times \left( \frac{28}{2} \right)^2 \]
\[ = \left( 28 \right)^2 + \frac{3}{2} \times \pi \times \left( \frac{28}{2} \right)^2 \]
\[ = \left( 28 \right)^2 \left( 1 + \frac{3}{2} \times \frac{22}{7} \times \frac{1}{2} \times \frac{1}{2} \right)\]
\[ = \left( 28 \right)^2 \left( 1 + \frac{33}{28} \right)\]
\[ = \left( 28 \right)^2 \times \frac{61}{28}\]
\[ = 28 \times 61\]
\[ = 1708 {cm}^2\]
Therefore, the area of the shaded region is 1708 cm2.
APPEARS IN
RELATED QUESTIONS
Find the area and perimeter of a square plot of land whose diagonal is 24 m long.
A road which is 7 m wide surrounds a circular park whose circumference is 352 m . Find the area of the road .
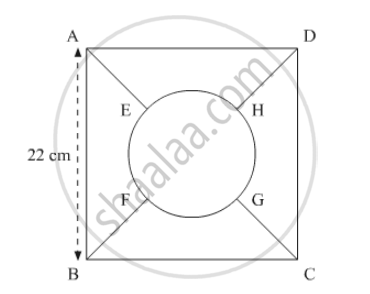
In the following figure, the square ABCD is divided into five equal parts, all having same area. The central part is circular and the ines AE, GC, BF and HD lie along the diagonals AC and BD of the square. If AB = 22 cm, find:
the circumference of the central part.
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

The perimeter of the sector OAB shown in the following figure, is

The area of a sector whose perimeter is four times its radius r units, is
If π is taken as `22/7` the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution, is
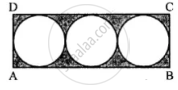
In the following figure, a rectangle ABCD enclosed three circles. If BC = 14 cm, find the area of the shaded portion (Take π = 22/7)
It is proposed to build a single circular park equal in area to the sum of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park would be ______.
Area of the circle obtained in 196 m2 is ______.
