Advertisements
Advertisements
Question
It is proposed to build a single circular park equal in area to the sum of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park would be ______.
Options
10 m
15 m
20 m
24 m
Solution
It is proposed to build a single circular park equal in area to the sum of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park would be 10 m.
Explanation:
Let D1 be the diameter of the first circular park = 16 m
∴ Radius R1 of first circular park = 8 m
Area of first circular park = πr2 = π(8)2 = 64 π m2
Let D2 be the diameter of the second circular park = 12 m
∴ Radius R2 of second circular park = 6 m
Area of second circular park = πr2 = π(6)2 = 36 π m2
Now, we are given that,
Area of single circular park = Area of first circular park + Area of second circular park
∴ πR2 = 64π + 36π = 100π ...(Where R is the radius of the single circular park)
πR2 = 100π
⇒ R2 = 100
⇒ R = 10
∴ Radius of the single circular park will be 10 m.
RELATED QUESTIONS
The dimensions of a room are 14 m x 10 m x 6.5 m There are two doors and 4 windows in the room. Each door measures 2.5 m x 1.2 m and each window measures 1.5 m x 1 m. Find the cost of painting the four walls of the room at ₹ `35perm^2` .
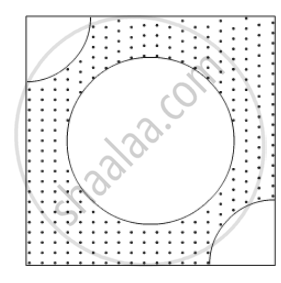
From each of the two opposite corners of a square of side 8 cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of radius 4.2 cm is also cut from the centre as shown in the following figure. Find the area of the remaining (Shaded) portion of the square. (Use π = 22/7)
In the following figure, two circles with centres A and B touch each other at the point C. If AC = 8 cm and AB = 3 cm, find the area of the shaded region.

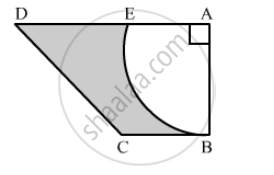
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm?
The length of the minute hand of a clock is 21 cm. The area swept by the minute hand in 10 minutes is
A circle of the largest area is cut from a rectangular piece of cardboard with dimensions 55 cm and 42 cm. Find the ratio between the area of the circle cut and the area of the remaining card-board.
A square is inscribed in a circle of radius 6 cm. Find the area of the square. Give your answer correct to two decimal places if `sqrt(2)` = 1.414.
Find the area of the biggest circle that can be cut from a rectangular piece 44cm by 28cm. also, find the area of the paper left after cutting out the circle.
The area of the circle whose diameter is 21 cm is ____________.
