Advertisements
Advertisements
Question
The length of the minute hand of a clock is 21 cm. The area swept by the minute hand in 10 minutes is
Options
231 cm2
210 cm2
126 cm2
252 cm2
Solution
Angle subtends by the minute hand in 1 minute = 6∘
∴ Angle subtends by the minute hand in 10 minutes = 60∘
Now,
Area of the sector`=theta/(360°) pi"r"^2 = 60°/360° xx 22/7(21)^2 = 231 "cm"^2`
Now,
Area of the sector`=theta/360°pi"r"^2 = (60°)/360^circxx22/7(21)^2=231 "cm"^2`
Hence, the correct answer is option (a).
APPEARS IN
RELATED QUESTIONS
In the given figure, ΔABC is an equilateral triangle the length of whose side is equal to 10 cm, and ΔADC is right-angled at D and BD= 8cm. Find the area of the shaded region.

A room is 16 m long and 13.5 m broad. Find the cost of covering its floor with 75-m-wide carpet at ₹ 60 per metre.
The area of sector is one-twelfth that of the complete circle. Find the angle of the sector .
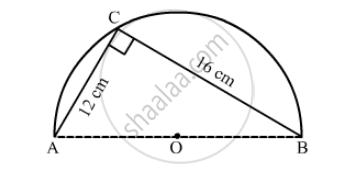
In the following figure, O is the centre of a circular arc and AOB is a straight line. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
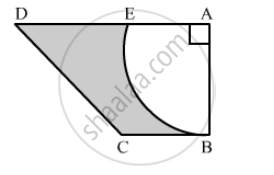
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
In the following figure, ABC is an equilateral triangle of side 8 cm. A, B and C are the centres of circular arcs of radius 4 cm. Find the area of the shaded region correct upto 2 decimal places. (Take π =3.142 and`sqrt3` = 1.732).

The ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal, is
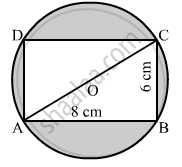
Find the area of the shaded region in the given figure, if ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle.
On decreasing the radius of a circle by 30%, its area is decreased by
If a square in inscribed in a circle, find the ratio of the areas of the circle and the square.
