Advertisements
Advertisements
Question
Find the area of the shaded region in the given figure, if ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle.
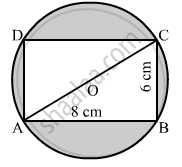
Solution
In right triangle ABC
AC2 = AB + BC2
= 82 + 62
= 64 + 36
= 100
∴ AC2 = 100
⇒ AC = 10 cm
Area of the shaded region = Area of circle − Area of rectangle OABC
`=> pi("OA")^2 -"AB"xx"BC"`
`⇒ 22/7xx(5)^2-8xx6`
= 78.57 - 48
= 30.57 cm2
Hence, the area of the shaded region is 30.57 cm2.
RELATED QUESTIONS
One side of a rectangle is 12 cm long and its diagonal measure 37 cm. Find the other side and the area of the rectangle.
A circle is inscribed in an equilateral triangle ABC is side 12 cm, touching its sides (the following figure). Find the radius of the inscribed circle and the area of the shaded part.

If the circumference and the area of a circle are numerically equal, then diameter of the circle is
The area of a circle whose area and circumference are numerically equal, is
ABCD is a rectangle whose three vertices are B (4,0), C (4,3) and D (0, 3). The length of one of its diagonals is
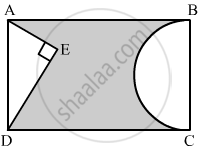
In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.
A chord of a circle of radius 10 cm subtends a right angle at the centre. The area of the minor segments (given, π = 3.14) is
The minute hand of a clock is 12 cm long. Find the area of the face of the clock described by the minute hand in 35 minutes.
Two circles touch each other externally. The sum of their areas is 74π cm2 and the distance between their centers is 12 cm. Find the diameters of the circle.
A pendulum swings through an angle of 30∘ and describes an arc 8.8 cm in length. Find the length of the pendulum in cm.
