Advertisements
Advertisements
Question
One side of a rectangle is 12 cm long and its diagonal measure 37 cm. Find the other side and the area of the rectangle.
Solution
One side of the rectangle = 12 cm
Diagonal of the rectangle = 37 cm
The diagonal of a rectangle forms the hypotenuse of a right-angled triangle. The other two sides of the triangle are the length and the breadth of the rectangle.
Now, using Pythagoras’ theorem, we have:
`"(One side)"^2+"(Other side)"^2="(hypotenuse)"^2`
⇒`(12)^2+"(other side)"^2=(37)^2`
⇒`144+(Other side)^2=1369`
⇒`(Other side)^2=1329-144`
⇒`(Other side)^2=1225`
⇒`(Other side)=sqrt1225`
⇒`Other side=35 cm`
Thus, we have:
Length = 35 cm
Breadth = 12 cm
Area of the rectangle=`35xx12=420 cm^2`
APPEARS IN
RELATED QUESTIONS
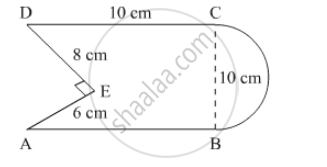
Find the area of the following figure, in square cm, correct to one place of decimal. (Take π = 22/7).
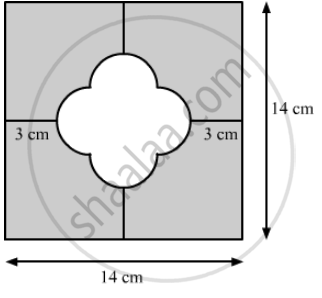
In the following figure find the area of the shaded region. (Use π = 3.14)
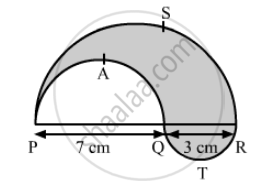
In the the following figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region.
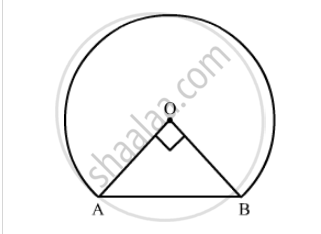
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the perimeter of the cross-section
If the radius of a circle is diminished by 10%, then its area is diminished by
If the perimeter of a sector of a circle of radius 6.5 cm is 29 cm, then its area is
A rope by which a cow is tethered is increased from 16 m to 23 m. How much additional ground does it have now graze?
If three circles of radius a each, are drawn such that each touches the other two, prove that the area included between them is equal to `4/25"a"^2`.
The following figure shows two circles with the same center. The radius of the larger circle is 10 cm and the radius of the smaller circle is 4 cm.

Find:
(a) the area of the larger circle
(b) the area of the smaller circle
(c) the shaded area between the two circles. (π = 3.14)
The area (in cm2) of the circle that can be inscribed in a square of side 8 cm is ____________.
