Advertisements
Advertisements
Question
In the following figure find the area of the shaded region. (Use π = 3.14)
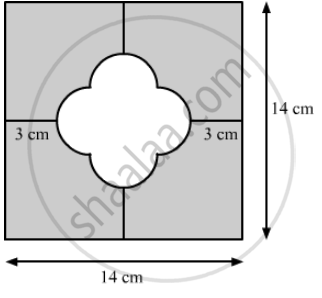
Solution
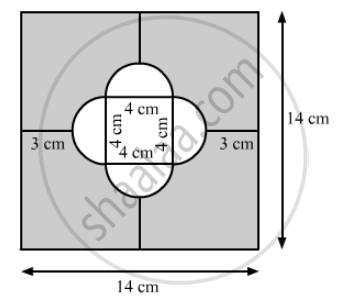
Area of shaded region = Area of square − Area of 4 semicircle having diameter 4 cm − Area of square having side 4 cm
\[= \left( Side \right)^2 - 4 \times \frac{1}{2}\pi r^2 - \left( side \right)^2 \]
\[ = \left( 14 \right)^2 - 2 \times 3 . 14 \times \left( \frac{4}{2} \right)^2 - 4^2 \]
\[ = 196 - 25 . 12 - 16\]
\[ = 154 . 88 {cm}^2\]
Hence, the area of shaded region is 154.88 cm2
APPEARS IN
RELATED QUESTIONS
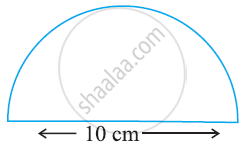
Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. `[\text{Use}pi=22/7]`
Find the area of the largest triangle that can be inscribed in a semi-circle of radius runits.
The ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal, is
If π is taken as `22/7` the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution, is
A wire when bent in the form of an equilateral triangle encloses an area of `121sqrt(3)" cm"^2`. If the same wire is bent into the form of a circle, what will be the area of the circle?
The floor of the circular swimming pool whose radius is 7 m has to be cemented at the rate of ₹ 18 per m2. Find the total cost of cementing the floor
It is proposed to build a single circular park equal in area to the sum of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park would be ______.
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is ______.
Area of the circle obtained in 196 m2 is ______.
