Advertisements
Advertisements
Question
A wire when bent in the form of an equilateral triangle encloses an area of `121sqrt(3)" cm"^2`. If the same wire is bent into the form of a circle, what will be the area of the circle?
Solution
Let a cm be the side of the equilateral triangle.
Now,
Area of the equilateral triangle`=sqrt(3)/4"a"^2`
We have:
`sqrt(3)/4"a"^2 = 121sqrt(3)`
`=> a^2/4 = 121`
⇒ a2 = 484
⇒ a = 22
Perimeter of the triangle = Circumference of the circle
Perimeter of the triangle = (22 + 22 + 22) cm
= 66 cm
Now, let r cm be the radius of the circle.
We know:
Circumference of the circle = 2πr
`=> 2xx22/7xx"r" = 66`
`=> "r"=(66xx7/44)"cm"`
`=> "r" = 21/2 "cm"`
Also,
Area of the circle = πr2
`=(22/7xx21/2xx21/2) "cm"^2`
`=693/2 "cm"^2`
= 346.5 cm2
APPEARS IN
RELATED QUESTIONS
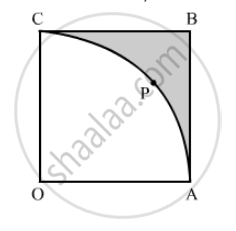
In the following figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. (Use π = 22/7)
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
If the circumference and the area of a circle are numerically equal, then diameter of the circle is
The ratio of the outer and inner perimeters of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then the radius of the circle
In the following figure, If ABC is an equilateral triangle, then shaded area is equal to
The areas of two concentric circles are 1386 cm2 and 962.5 cm2. The width of the ring is
The circumference of a circular table is 88 m. Find its area.
The formula used to find the area of the circle is ________ sq.units
A pendulum swings through an angle of 30∘ and describes an arc 8.8 cm in length. Find the length of the pendulum in cm.
