Advertisements
Advertisements
Question
In the following figure, the square ABCD is divided into five equal parts, all having same area. The central part is circular and the lines AE, GC, BF and HD lie along the diagonals AC and BD of the square. If AB = 22 cm, find:
the perimeter of the part ABEF.

Solution
We have a square ABCD.
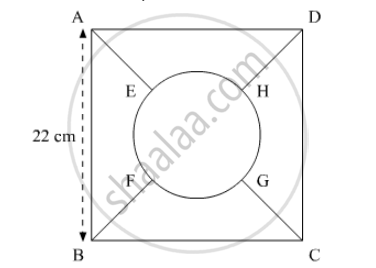
We have to find the perimeter of ABEF. Let O be the centre of the circular region.
Use Pythagoras theorem to get,
`2(AE+r)^2=22^2`
`AE+r=15.56`
`AE=(15.56-5.56)cm`
`= 10c,`
Similarly,
`BF=10cm`
Now length of arc EF,
`= "perimeter of circular region"/4`
`= 34.88/4 cm`
So, perimeter of ABFE,
`=AB+BF+EF+AE`
`=(22+10+8.64+10)`
`= 50.64`
APPEARS IN
RELATED QUESTIONS
Find the area of the following circles, given that radius = 5 cm.
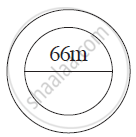
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
A 36-m-long, 15-m-borad verandah is to be paved with stones, each measuring 6dm by 5 dm. How many stones will be required?
The length and breadth of a rectangular garden are in the ratio 9:5. A path 3.5 m wide, running all around inside it has an area of `1911m^2` . Find the dimensions of the garden.
In the following figure, PQRS is a square of side 4 cm. Find the area of the shaded square.
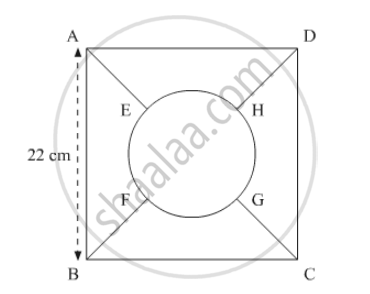
In the following figure, the square ABCD is divided into five equal parts, all having same area. The central part is circular and the ines AE, GC, BF and HD lie along the diagonals AC and BD of the square. If AB = 22 cm, find:
the circumference of the central part.
From a thin metallic piece, in the shape of a trapezium ABCD, in which AB || CD and ∠BCD = 90°, a quarter circle BEFC is removed (in the following figure). Given AB = BC = 3.5 cm and DE = 2 cm, calculate the area of the remaining piece of the metal sheet.
The area of incircle of an equilateral triangle is 154 cm2 . The perimeter of the triangle is
The area of a sector of a circle with radius r, making an angle of x° at the centre is
A circle of the largest area is cut from a rectangular piece of cardboard with dimensions 55 cm and 42 cm. Find the ratio between the area of the circle cut and the area of the remaining card-board.
