Advertisements
Advertisements
Question
The length and breadth of a rectangular garden are in the ratio 9:5. A path 3.5 m wide, running all around inside it has an area of `1911m^2` . Find the dimensions of the garden.
Solution
Let the length and breadth of the garden be 9x m and 5x m, respectively, Now,
Area of the garden=`(9x xx 5x)45x^2`
Length of the garden excluding the path =`(9x-7)`
Breadth of the garden excluding the path =`(5x-7)`
Area of the path = `45x^2=[(9x-7)(5x-7)]`
⇒ `1911=45x^2-[45x^2-63x-35x+49]`
⇒`1911=45x^2-45x^2+63x+35x-49`
⇒`1911=98x-49`
⇒`1960=98x`
⇒`x=1960/98`
⇒ `x=20`
Thus, we have:
Length=`9x=20xx9=180m`
Breadth=`5x=5xx20=100m`
APPEARS IN
RELATED QUESTIONS
Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹ 15/m2. (Take π = 3.14)
What is the angle subtended at the centre of a circle of radius 6 cm by an arc of length 3 π cm?
If the difference between the circumference and radius of a circle is 37 cm, then using π = \[\frac{22}{7}\] the circumference (in cm) of the circle is
If the area of the circle is numerically equal to twice its circumference then what is the diameter of the circle?
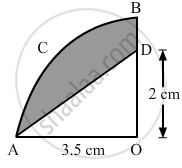
In the given figure, OABC is a quadrant of a circle of radius 3.5 cm with centre O. If OD = 2 cm, find the area of the shaded portion.
In the given figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region. [Use π= 3.14]

If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
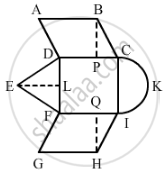
A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure.
Two circles touch each other externally. The sum of their areas is 58π cm2 and the distance between their centers is 10 cm. Find the radii of the two circles.
A wire, when bent in the form of a square; encloses an area of 196 cm2. If the same wire is bent to form a circle; find the area of the circle.
