Advertisements
Advertisements
Question
In the given figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region. [Use π= 3.14]

Solution
Perimeter of shaded region = Length of the arc PAQ + Length of the arc PSR + Length of the arc RTQ
`=1/2xx2pi"r"_1 + 1/2 xx 2pi"r"_2 + 1/2xx 2pi"r"_3`
`=1/2xx2pi(7/2)+1/2xx2pi(10/2)+1/2xx2pi(3/2)`
`=7/2pi + 5pi + 3/2pi`
`=7/2pi+3/2pi+5pi`
=5π + 5π
= 10π
= 31.4 cm
Hence, the perimeter of shaded region is 31.4 cm.
APPEARS IN
RELATED QUESTIONS
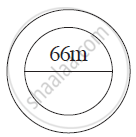
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
What is the angle subtended at the centre of a circle of radius 6 cm by an arc of length 3 π cm?
Write the formula for the area of a sector of angle \[\theta\] (in degrees) of a circle of radius r.
If he area of a sector of a circle is \[\frac{7}{20}\] of the area of the circle, then the sector angle is equal to
ABCD is a square of side 4 cm. If E is a point in the interior of the square such that ΔCEDis equilateral, then area of Δ ACE is
A square is inscribed in a circle of radius 7 cm. Find the area of the square.
Two circles touch each other externally. The sum of their areas is 58π cm2 and the distance between their centers is 10 cm. Find the radii of the two circles.
Find the area of the shaded portion in each of the following diagrams:
(i)

(ii)

The radii of the inner and outer circumferences of a circular running track are 63 m and 70 m respectively. Find :
(i) the area of the track ;
(ii) the difference between the lengths of the two circumferences of the track.
