Question

ABCD is a square of side 4 cm. If E is a point in the interior of the square such that ΔCEDis equilateral, then area of Δ ACE is

Options

• \[2\sqrt{3} - 1 c m^2\]

• \[4\sqrt{3} - 1 c m^2\]

• \[6\sqrt{3} - 1 c m^2\]

• \[8\sqrt{3} - 1 c m^2\]

Answer 1

We have the following diagram. 

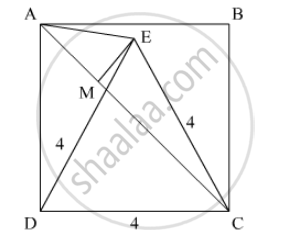
Since `ΔCED` is equilateral,

Therefore, 

`EC=CD=DE=4 cm`

Now, `∠ ECD=60°`

Since AC is diagonal of sqr.ABCD

Therefore, 

`∠ACD=45°`

Therefore we get,

`∠ECA=∠ECD-∠ACD`

         `=60°-45°`

        `=15°`

Now, in `ΔACE`, draw a perpendicular EM to the base AC.

So in `Δ EMC`

`sin 15°=(EM)/(EC)`

`=(EM)/4` 

Therefore,

`EM=sqrt2(sqrt3-1)` 

Now in `ΔAEC`

ar `(ΔAEC=1/2) (AC)(EM)`

              `=4(sqrt3-1)cm^2`