Advertisements
Advertisements
Question
The radius of a circle is 20 cm. It is divided into four parts of equal area by drawing three concentric circles inside it. Then, the radius of the largest of three concentric circles drawn is
Options
10 \[\sqrt{5}\]
10\[\sqrt{3}\]cm
10\[\sqrt{5}\]
10\[\sqrt{2}\]
Solution
The circle can be divided into four parts of equal area by drawing three concentric circles inside it as,

It is given that OB = 20 cm. Let OA = x.
Since the circle is divided into four parts of equal area by the three concentric circles, we have,
Area of the fourth region `=1/4xx`Area of the given circle
`pixx(20^2-x^2)=1/4xxpixx20^2`
`400-x^2=100`
`x^2=300`
`x-10sqrt3 cm`
APPEARS IN
RELATED QUESTIONS
Find the area of a parallelogram with base equal to 25 cm and the corresponding height measuring 16.8 cm.
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of π, is
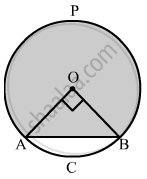
Find the area of the major segment APB of a circle of radius 35 cm and ∠AOB = 90°, as shown in the given figure.
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made.
A chord of a circle of radius 14 cm a makes a right angle at the centre. Find the area of the sector.
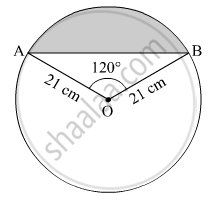
Find the area of the segment shown in Fig. 2, if the radius of the circle is 21 cm and ∠AOB = 120° `( "Use" π = (22)/(7))`
There is a path of uniform width 7 m round and outside a circular garden of diameter 210 m. Find the area of the path.
The ratio of the area of a circle to the area of its semicircle is
Find the area of the shaded region: