Advertisements
Advertisements
Question
If he area of a sector of a circle is \[\frac{7}{20}\] of the area of the circle, then the sector angle is equal to
Options
110°
130°
100°
126°
Solution
We have given that area of the sector is `7/20`
of the area of the circle.
Therefore, area of the sector =` 7/20xx` area of the circle
`∴ θ/360xxpir^2=7/20xxpir^2`
Now we will simplify the equation as below,
`θ/360=7/20`
Now we will multiply both sides of the equation by 360,
`∴ θ=7/20xx360`
Therefore, sector angle is `126°`
APPEARS IN
RELATED QUESTIONS
One side of a rectangle is 12 cm long and its diagonal measure 37 cm. Find the other side and the area of the rectangle.
The area of sector is one-twelfth that of the complete circle. Find the angle of the sector .
In the following figure, PQRS is a square of side 4 cm. Find the area of the shaded square.
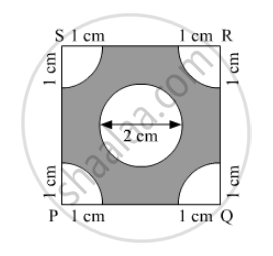
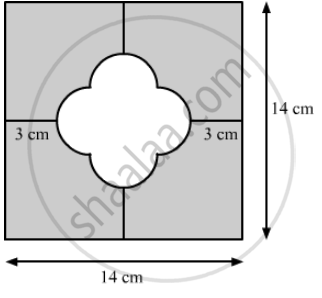
In the following figure find the area of the shaded region. (Use π = 3.14)
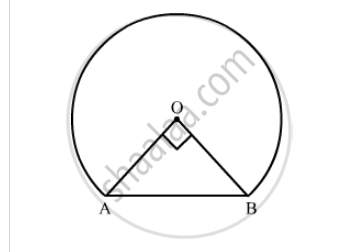
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the height of the tunnel
Write the formula for the area of a sector of angle \[\theta\] (in degrees) of a circle of radius r.
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then its radius is
The radius of a circle is 20 cm. It is divided into four parts of equal area by drawing three concentric circles inside it. Then, the radius of the largest of three concentric circles drawn is
The area of the sector of angle θ° of a circle with radius R is
The sum of the radii of two circles is 10.5 cm and the difference of their circumferences is 13.2 cm. Find the radii of the two circles.
