Advertisements
Advertisements
प्रश्न
If he area of a sector of a circle is \[\frac{7}{20}\] of the area of the circle, then the sector angle is equal to
पर्याय
110°
130°
100°
126°
उत्तर
We have given that area of the sector is `7/20`
of the area of the circle.
Therefore, area of the sector =` 7/20xx` area of the circle
`∴ θ/360xxpir^2=7/20xxpir^2`
Now we will simplify the equation as below,
`θ/360=7/20`
Now we will multiply both sides of the equation by 360,
`∴ θ=7/20xx360`
Therefore, sector angle is `126°`
APPEARS IN
संबंधित प्रश्न
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB=90° and AC = 15 cm.

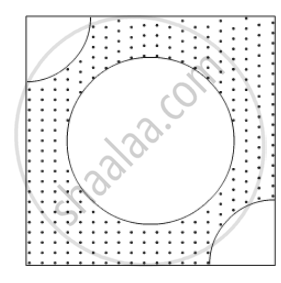
From each of the two opposite corners of a square of side 8 cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of radius 4.2 cm is also cut from the centre as shown in the following figure. Find the area of the remaining (Shaded) portion of the square. (Use π = 22/7)
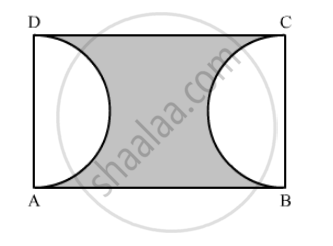
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
In the following figure, the square ABCD is divided into five equal parts, all having same area. The central part is circular and the lines AE, GC, BF and HD lie along the diagonals AC and BD of the square. If AB = 22 cm, find:
the perimeter of the part ABEF.

If the sum of the areas of two circles with radii r1 and r2 is equal to the area of a circle of radius r, then \[r_1^2 + r_2^2\]
In the following figure, If ABC is an equilateral triangle, then shaded area is equal to
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
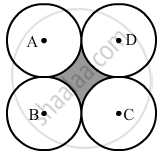
Four equal circles, each of radius 5 cm, touch each other, as shown in the figure. Find the area included between them.
The diameter of a wheel is 40 cm. How many revolutions will it make in covering 176 m?
Find the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm.
