Advertisements
Advertisements
Question
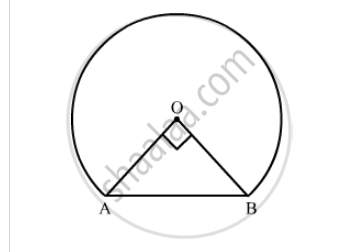
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the height of the tunnel
Solution
We have a cross section of a railway tunnel. `ΔOAB`is a right angled isosceles triangle, right angled at O. let OM be perpendicular to AB.
`OA=2 m`
Use Pythagoras theorem in `ΔOAB`to get,
`AB=(sqrt(2^2+2^2))m`
`= 2sqrt2 m`
Let the height of the tunnel be h. So,
`"Area of" ΔOAB=1/2(2)(2)`
`1/2(2sqrt2)(OM)=2`
Thus,
`OM=sqrt2m`
Therefore,
`h=(2+sqrt2)m`
APPEARS IN
RELATED QUESTIONS
The area of rectangle is `192cm^2` and its perimeter is 56 cm. Find the dimensions of the rectangle.
Find the area of a parallelogram with base equal to 25 cm and the corresponding height measuring 16.8 cm.
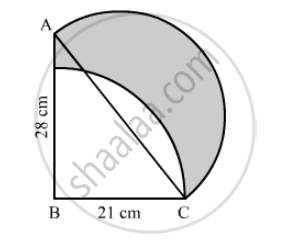
In the following figure, ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
The area of the largest triangle that can be inscribed in a semi-circle of radius r is
The area of a sector of a circle with radius r, making an angle of x° at the centre is
Find the radius and area of a circle, whose circumference is :
(i) 132 cm
(ii) 22 m
The circumference of a circular table is 88 m. Find its area.
The area (in cm2) of the circle that can be inscribed in a square of side 8 cm is ____________.
The area of the circle whose diameter is 21 cm is ____________.
How much distance, in metres, a wheel of 25 cm radius will cover if it rotates 350 times?
