Advertisements
Advertisements
प्रश्न
In the given figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region. [Use π= 3.14]

उत्तर
Perimeter of shaded region = Length of the arc PAQ + Length of the arc PSR + Length of the arc RTQ
`=1/2xx2pi"r"_1 + 1/2 xx 2pi"r"_2 + 1/2xx 2pi"r"_3`
`=1/2xx2pi(7/2)+1/2xx2pi(10/2)+1/2xx2pi(3/2)`
`=7/2pi + 5pi + 3/2pi`
`=7/2pi+3/2pi+5pi`
=5π + 5π
= 10π
= 31.4 cm
Hence, the perimeter of shaded region is 31.4 cm.
APPEARS IN
संबंधित प्रश्न
Prove that the area of a circular path of uniform width h surrounding a circular region of radius r is `pih(2r+h)`
From a circular piece of cardboard of radius 3 cm two sectors of 900 have been cutoff . Find the perimeter of the remaining portion nearest hundredth centimeters ( `"Take" pi = 22/ 7`).
A circular field has a perimeter of 650 m. A square plot having its vertices on the circumference of the field is marked in the field. Calculate the area of the square plot.
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
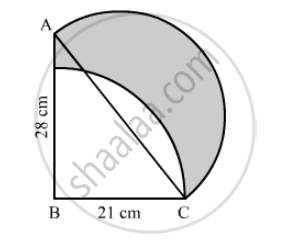
In the following figure, ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
In the following figure, AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.

If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then its radius is
From a rectangular sheet of paper ABCD with AB = 40 cm and AD = 28 cm, a semicircular portion with BC as diameter is cut off. Find the area of the remaining paper.
Find the radius and area of a circle, whose circumference is :
(i) 132 cm
(ii) 22 m
Find the area enclosed between two concentric circles, If their radii are 6cm and 13cm respectively.
