Advertisements
Advertisements
प्रश्न
A circular field has a perimeter of 650 m. A square plot having its vertices on the circumference of the field is marked in the field. Calculate the area of the square plot.
उत्तर
We have a circular field in which a square field is marked.
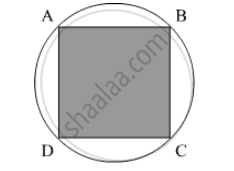
Let the radius of the circle be r. We have,
Perimeter=`650`
`2pi r=650`
`= r=325/pi`
Use Pythagoras theorem to find the side of square as,
`AB=sqrt(r^2+r^2)`
`=325/pi sqrt2`
So area of the square plot,
`=(AB)^2`
`=(325/pi sqrt2)^2 m^2`
`=((325(7))/22 sqrt2)^2 m^2`
`= 21387 m^2`
APPEARS IN
संबंधित प्रश्न
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.
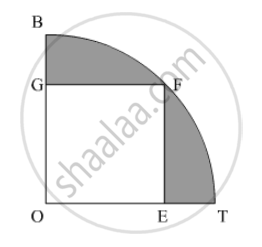
In the following figure, OE = 20 cm. In sector OSFT, square OEFG is inscribed. Find the area of the shaded region.
ABCDEF is a regular hexagon with centre O (in the following figure). If the area of triangle OAB is 9 cm2, find the area of : (i) the hexagon and (ii) the circle in which the haxagon is incribed.
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the perimeter of the cross-section
If the perimeter of a semi-circular protractor is 36 cm, then its diameter is
If the area of a sector of a circle is `5/18` of the area of the circle, then the sector angle is equal to
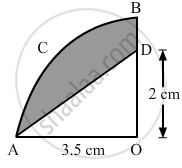
In the given figure, OABC is a quadrant of a circle of radius 3.5 cm with centre O. If OD = 2 cm, find the area of the shaded portion.
Find the lengths of the arcs cut off from a circle of radius 12 cm by a chord 12 cm long. Also, find the area of the minor segment.
In the given figure, ABCD is a square each of whose sides measures 28 cm. Find the area of the shaded region.

A square tank has an area of 1600 cm2. There are four semicircular plots around it. Find the cost of turfing the plots at Rs 12.50 per m2
